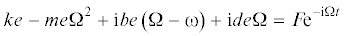Известия РАН. Механика твердого тела, 2022, № 6, стр. 41-53
САМОВОЗБУЖДАЮЩИЕСЯ КОЛЕБАНИЯ МАЛОВЯЗКОЙ ЖИДКОСТИ И ИХ ВЛИЯНИЕ НА РОТОР С МАЛЫМ ЧИСЛОМ РАДИАЛЬНЫХ ПЕРЕГОРОДОК
a Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: n.andre@mail.ru
Поступила в редакцию 20.10.2021
После доработки 19.12.2021
Принята к публикации 21.12.2021
- EDN: YLNCGR
- DOI: 10.31857/S0572329922050105
Аннотация
Предложена теория (математическая модель) прецессии гибкого ротора с полостью, равноразделенной радиальными перегородками и частично заполненной маловязкой жидкостью. Самовозбуждающиеся во вращающемся и прецессирующем роторе с малым числом перегородок (от 1 до 3) колебания жидкости приводят к специфическим частотам системы и динамической неустойчивости в диапазоне, не связанном с обычной синхронной критической скоростью.
1. Введение. Известно, что вибрации центрифуг, сепараторов, охлаждаемых изнутри газовых турбин, поплавковых гироскопов, вращающихся ракет и автобалансирующих устройств с частичным жидкостным наполнением, а также иных роторов, внутрь которых случайно проникла жидкость, могут быть значительными на некоторых скоростях вращения вследствие волнообразования [1–4]. Между тем, говорить о том, что тема построений для самовозбуждающихся колебаний ротора, частично заполненного маловязкой жидкостью, аналитических моделей и решений [5–8] закрыта, преждевременно. Так, для гашения колебаний жидкости применяются радиальные перегородки, и поскольку соответствующие системы описать математически и в общем виде затруднительно, ограничиваются численным (как правило конечно-элементным) модальным анализом. На практике на основе накопленного опыта эксплуатации распространен тривиальный подход к подавлению волн – чем больше радиальных перегородок, тем лучше, т.е. фактически не занимаются поиском/оптимизацией относительно малого и достаточного числа перегородок под конкретную роторную машину.
Пусть простейший симметричный полый ротор в виде двухопорного гибкого вала с цилиндрической полостью посередине в отличие от предшественников [9–13] имеет внутри несколько радиальных перегородок, причем образованные ими отсеки одинаковы, частично и равно заполнены несжимаемой маловязкой жидкостью, и вся эта роторная система вращается с постоянной угловой скоростью ω.
2. Задача движения ротора с маловязкой жидкостью и радиальными перегородками. В случае вертикальной ориентировки, уравновешенности и невозмущенного (чистого) вращения такой системы ротор движется вместе с жидкостью как одно твердое тело вне зависимости от вязкости. Пусть относительно этого динамического равновесия колебания ротора и жидкости малы, т.е. возмущенным движением ротора является прецессия его геометрического центра с отличной от ω угловой скоростью Ω и малым радиусом e, а возмущенным движением жидкости являются малые перемещения ее некоторых частиц с линейными скоростями $u$, ${v}$ относительно ротора (рис. 1), в т.ч. с малым отклонением ε свободной ее поверхности от внутреннего радиуса r гипотетической жидкости, затвердевшей при чистом вращении системы (пунктирная окружность на рис. 1).
Рис. 1.
Динамическая модель симметричного гибкого ротора с полостью, разделенной сплошными радиальными перегородками, частично и равно заполненной маловязкой жидкостью, а также плоских распространяющихся в окружном направлении волн, например как показано 2-го порядка (κ = 2, n = 3, k = nκ, λk = 2πr/k).

Здесь и далее приняты допущения, что числа Рейнольдса, Фруда и Бонда достаточно велики, т.е. что эффекты вязкости, поверхностного натяжения и гравитации пренебрежимо слабо отражаются на поведении пограничных слоев жидкости. Таким образом, жидкость рассматривается как идеальная, однослойная и невесомая. Условия, при которых это возможно: ωr2$ \gg $ ν, ρr3ω2$ \gg $ σ и rω2$ \gg $ g (когда ось роторной системы сориентирована вертикально) или r2ω2$ \gg $ gL (когда – горизонтально), где ν, ρ и σ – кинематическая вязкость, плотность и коэффициент поверхностного натяжения жидкости, g – гравитационное ускорение, L – размер полости вдоль собственной оси.
Асинхронную прецессию ротора удобно анализировать в неподвижной цилиндрической системе координат $e\psi Z$ с началом в геометрическом центре полости при недеформированном вале ротора, так что ось Z есть линия центров подшипников. Колебания вращающейся жидкости удобно исследовать в жестко связанной с ротором цилиндрической системе координат rθz, начало которой находится в центре полости деформированного ротора, а также с осью z, параллельной оси Z.
Со введением неподвижных декартовой XYZ и цилиндрической $e\psi Z$, а также движущихся вместе с ротором прямоугольной xyz и цилиндрической rθz систем отсчета динамическая модель полого секторированного ротора с жидкостью принимает вид (рис. 1).
В рассматриваемой системе пустой ротор имеет массу m. Подшипники являются жесткими по сравнению с валом, обладающим изгибной жесткостью k. Внутреннее и внешнее демпфирование ротора, включая трение в подшипниках, характеризуются коэффициентами b и d соответственно. В такой формулировке как известно [14], уравнения движения гибкого симметричного ротора имеют вид:
То же самое, вводя удобное комплексное представление отклонений Z = X + iY:
Путем подстановки ${\text{Z}} = e{{{\text{e}}}^{{{\text{i}}\psi }}}$ можно выразить уравнение прецессии заданного ротора в полярных координатах e, $\psi $:
(2.1)
$m(\ddot {e} + {\text{i}}e\ddot {\psi } + {\text{i}}2\dot {e}\dot {\psi } - e{{\dot {\psi }}^{2}}) + \left( {b + d} \right)\dot {e} + ke + {\text{i}}de\dot {\psi } + {\text{i}}be\left( {\dot {\psi } - \omega } \right) = F{{{\text{e}}}^{{ - {\text{i}}\psi }}}$Составляющие гидродинамической силы F есть интегральные величины (суммы) проекций на неподвижные оси X и Y давлений жидкости на всей поверхности S боковой стенки полости:
(2.2)
${{F}_{X}} = \int\limits_S {{{{\text{p}}}_{{{\text{r}} = R}}}\cos ({{\omega }}t + {{\theta }})dS} ,\quad {{F}_{Y}} = \int\limits_S {{{{\text{p}}}_{{{\text{r}} = R}}}\sin ({{\omega }}t + {{\theta }})dS} ,\quad {\text{где}}\quad dS = RLd\theta $Соответственно, гидродинамические составляющие в направлениях подвижных осей х и у:
Очевидно, анализ движения ротора, содержащего жидкость, требует решения совместной задачи теории колебаний и гидродинамики. Гидродинамическая сторона задачи сводится к отысканию поля давлений в наиболее общем случае с помощью уравнений Навье–Стокса и неразрывности. Согласно им, течение вязкой жидкости, свободной от массовых и поверхностных сил, вращающейся со скоростью ротора ω и в то же время прецессирующей вместе с ним со скоростью $\dot {\psi }$ (рис. 1) будут определять уравнения [15, 16]:
(2.3)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} - \nu \left( {\frac{{{{\partial }^{2}}u}}{{\partial {{r}^{2}}}} + \frac{{\partial u}}{{r\partial r}} + \frac{{{{\partial }^{2}}u}}{{{{r}^{2}}\partial {{\theta }^{2}}}} - \frac{u}{{{{r}^{2}}}} - 2\frac{{\partial {v}}}{{{{r}^{2}}\partial \theta }}} \right) + u\frac{{\partial u}}{{\partial r}} + {v}\frac{{\partial u}}{{r\partial \theta }} - \\ - \;\frac{{{{{v}}^{2}}}}{r} - {{\omega }^{2}}r - 2\omega {v} = - \frac{{\partial p}}{{\rho \partial r}} - \ddot {X}\cos \left( {\omega t + \theta } \right) - \ddot {Y}\sin \left( {\omega t + \theta } \right) \\ \frac{{\partial {v}}}{{\partial t}} - \nu \left( {\frac{{{{\partial }^{2}}{v}}}{{\partial {{r}^{2}}}} + \frac{{\partial {v}}}{{r\partial r}} + \frac{{{{\partial }^{2}}{v}}}{{{{r}^{2}}\partial {{\theta }^{2}}}} - \frac{{v}}{{{{r}^{2}}}} + 2\frac{{\partial u}}{{{{r}^{2}}\partial \theta }}} \right) + u\frac{{\partial {v}}}{{\partial r}} + {v}\frac{{\partial {v}}}{{r\partial \theta }} + \\ + \;\frac{{u{v}}}{r} + 2\omega u = - \frac{{\partial p}}{{\rho r\partial \theta }} + \ddot {X}\sin \left( {\omega t + \theta } \right) - \ddot {Y}\cos \left( {\omega t + \theta } \right) \\ r\frac{{\partial u}}{{\partial r}} + u + \frac{{\partial {v}}}{{\partial \theta }} = 0 \\ \end{gathered} $Члены с множителем ω2 и 2ω учитывают влияние нормального ускорения и ускорения Кориолиса от вращения ротора, а члены с множителем $\ddot {X}$ и $\ddot {Y}$ характеризуют эффект переносного ускорения начала отсчета жестко связанной с ротором системы координат за счет его прецессии.
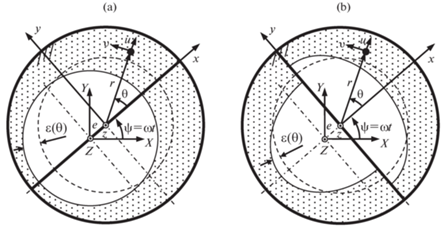
Заданная система уравнений (2.3) не включает компоненты и отдельное уравнение по z-координате жидкостной частицы. Обоснование для их отсутствия видится в конфигурации жидкости при синхронной прецессии полости ($\dot {\psi } = \Omega = \omega $), и наиболее четко на примере с двумя герметичными перегородками, коллинеарными и перпендикулярными направлению роторного смещения e. На рис. 2, а кружение перегородок вокруг оси Z не препятствует образованию общей округлой свободной поверхности жидкости, как при отсутствии перегородок. На рис. 2, b “лунное” движение перегородок максимально препятствует этому, порождая две различные примерно полуэллиптические жидкостные поверхности. Здесь также малое роторное отклонение e вызывает малое отклонение ε свободной поверхности жидкости от внутреннего радиуса r гипотетической, затвердевшей при чистом вращении системы. В случае несинхронного (с вращением) прецессионного движения инициируется непрерывное переливание и видоизменение между первой и второй отмеченными плоскими конфигурациями. Как следствие, возмущение асинхронной прецессией не сопровождается появлением относительных скоростей частиц жидкости (относительно стенок полости) в z-направлении.
Рис. 2.
Возможные фиксированные конфигурации вращающейся жидкости в синхронно прецессирующем роторе.
Возмущенные скорости $u$, ${v}$ сопряжены с возмущенным давлением p, увеличивающим стационарное p0, которое пропорционально квадрату скорости вращения ω2. По аналогии с гидростатическим давлением столба жидкости, в заданной системе ускорение = ω2(r + r)/2, а высота = r – r. Таким образом, без потери общности, давление в жидкости:
(2.4)
$p = {{p}_{0}} + p\left( {{\text{r}},{{\theta }},t} \right),\quad {\text{где}}\quad {{p}_{0}} = {{{{\rho }}{{{{\omega }}}^{2}}({{r}^{2}} - {{r}^{2}})} \mathord{\left/ {\vphantom {{{{\rho }}{{{{\omega }}}^{2}}({{r}^{2}} - {{r}^{2}})} 2}} \right. \kern-0em} 2}$Похожим образом определяется свободная поверхность жидкости:
где ε – ее возмущенное смещение.Граничные условия, дополняющие (2.3), т.е. задающие поведение уравнений (2.3) на поверхностях жидкости:
При этом, если подставить (2.5) в (2.4), а именно в p0 вместо r, и отбросить квадрат малого, т.е. величину ε2, то ${\text{p}} = {{\rho }}{{{{\omega }}}^{2}}r{{\varepsilon }} + p\left( {{\text{r}},{{\theta }},t} \right)$ и ${{p}_{{{\text{r}} = r}}} = - {{\rho }}{{{{\omega }}}^{2}}r{{\varepsilon }}$, а ключевые кинематические и динамические граничные условия могут быть преобразованы к виду:
(2.6)
${{u}_{{{\text{r}} = R}}} = 0,\quad {{\partial {{p}_{{{\text{r}} = r}}}} \mathord{\left/ {\vphantom {{\partial {{p}_{{{\text{r}} = r}}}} {\partial t}}} \right. \kern-0em} {\partial t}} = - {{\rho }}{{{{\omega }}}^{2}}r{{u}_{{{\text{r}} = r}}}$Задача состоит в отыскании решений (законов) таких движений, которые представляют собой малое незатухающее периодическое+переносное отклонение жидкости в окружном направлении от ее установившегося состояния вращения как твердого тела. В этом случае можно пренебречь в уравнениях (2.3) вязкими компонентами и скоростными членами второго порядка малости, а также с учетом (2.4) в первом приближении получить:
При умножении второго уравнения на мнимую единицу и сложении первых двух уравнений, а затем при умножении первого уравнения на мнимую единицу и вычитании из него второго уравнения, они преобразуются в:
(2.7)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} - 2\omega {v} + i\frac{{\partial {v}}}{{{v}t}} + i2\omega u = - \frac{{\partial p}}{{\rho \partial r}} - i\frac{{\partial p}}{{\rho r\partial \theta }} - \ddot {Z}{{e}^{{ - i(\omega t + \theta )}}} \\ i\frac{{\partial u}}{{\partial t}} - i2\omega {v} - \frac{{\partial {v}}}{{\partial t}} - 2\omega u = - i\frac{{\partial p}}{{\rho \partial r}} + \frac{{\partial p}}{{{{\rho r}}\partial \theta }} - {\text{i}}\ddot {Z}{{e}^{{ - i(\omega t + \theta )}}} \\ \end{gathered} $3. Решение уравнений стационарного движения системы “ротор–жидкость”. В случае установившейся прецессии $\psi = {{\Omega }}t$, e = const,  , т.е. системные уравнения (2.1) и (2.7) принимают вид:
, т.е. системные уравнения (2.1) и (2.7) принимают вид:
(3.2)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} - 2{{\omega }}{v} = - \frac{{\partial p}}{{{{\rho }}\partial {\text{r}}}} + e{{{{\Omega }}}^{2}}{{{\text{e}}}^{{{\text{i(}}{{{{\Omega }}}_{0}}t - {{\theta )}}}}} \\ \frac{{\partial {v}}}{{\partial t}} + 2{{\omega }}u = - \frac{{\partial p}}{{{{\rho r}}\partial {{\theta }}}} - {\text{i}}e{{{{\Omega }}}^{2}}{{{\text{e}}}^{{{\text{i(}}{{{{\Omega }}}_{0}}t - {{\theta )}}}}} \\ {\text{r}}\frac{{\partial u}}{{\partial {\text{r}}}} + u + \frac{{\partial {v}}}{{\partial {{\theta }}}} = 0,\quad {\text{где}}\quad {{{{\Omega }}}_{0}} = {{\Omega }} - {{\omega }} \\ \end{gathered} $Если предположить, что:
(3.3)
$\begin{array}{*{20}{c}} {{{\varepsilon }}\left( {{{\theta }},t} \right) = {{\varepsilon }}({{\theta }}){{\operatorname{e} }^{{{\text{i}}{{{{\Omega }}}_{0}}t}}}} \\ {p\left( {{\text{r}},{{\theta }},t} \right) = {\text{P}}({\text{r}},{{\theta }}){{\operatorname{e} }^{{{\text{i}}{{{{\Omega }}}_{0}}t}}}} \\ {u\left( {{\text{r}},{{\theta }},t} \right) = {\text{U}}({\text{r}},{{\theta }}){{\operatorname{e} }^{{{\text{i}}{{{{\Omega }}}_{0}}t}}}} \\ {{v}\left( {{\text{r}},{{\theta }},t} \right) = {\text{V}}({\text{r}},{{\theta }}){{\operatorname{e} }^{{{\text{i}}{{{{\Omega }}}_{0}}t}}}} \end{array}$Решения первых двух из этих уравнений следующие:
С этими выражениями третье уравнение (неразрывности) дает:
Чтобы найти С1 и С2, следует перейти от U к U(r), производя в (3.4) замены $\frac{{\partial {\text{P}}}}{{\partial {\text{r}}}} = \frac{{\partial P({\text{r}})}}{{\partial {\text{r}}}}\,{{{\text{e}}}^{{ - {\text{i}}n{{\theta }}}}}$ и $\frac{{\partial {\text{P}}}}{{\partial {{\theta }}}} = - {\text{i}}nP({\text{r}})\,{{{\text{e}}}^{{ - {\text{i}}n{{\theta }}}}}$, т.е.:
Раскрытие здесь P(r) и ${{\partial P({\text{r}})} \mathord{\left/ {\vphantom {{\partial P({\text{r}})} {\partial {\text{r}}}}} \right. \kern-0em} {\partial {\text{r}}}}$ через равенство (3.5) приводит к выражениям:
(3.6)
$\begin{gathered} U({\text{r}}) = {\text{i}}\frac{n}{{{\rho }}}\left( {\frac{{{{C}_{1}}{{{\text{r}}}^{{n - 1}}}}}{{{{{{\Omega }}}_{0}} + 2{{\omega }}}} - \frac{{{{C}_{2}}{{{\text{r}}}^{{ - n - 1}}}}}{{{{{{\Omega }}}_{0}} - 2{{\omega }}}}} \right) - {\text{i}}\frac{{e{{{{\Omega }}}^{2}}}}{{{{{{\Omega }}}_{0}} + 2{{\omega }}}}{{{\text{e}}}^{{{\text{i(}}n - 1){{\theta }}}}} \\ V({\text{r}}) = \frac{n}{{{\rho }}}\left( {\frac{{{{C}_{1}}{{{\text{r}}}^{{n - 1}}}}}{{{{{{\Omega }}}_{0}} + 2{{\omega }}}} + \frac{{{{C}_{2}}{{{\text{r}}}^{{ - n - 1}}}}}{{{{{{\Omega }}}_{0}} - 2{{\omega }}}}} \right) - \frac{{e{{{{\Omega }}}^{2}}}}{{{{{{\Omega }}}_{0}} + 2{{\omega }}}}{{{\text{e}}}^{{{\text{i(}}n - 1){{\theta }}}}} \\ \end{gathered} $Условие U(R) = 0 и (3.6) определяют, что
(3.7)
${{C}_{2}} = {{C}_{1}}\frac{{{{{{\Omega }}}_{0}} - 2{{\omega }}}}{{{{{{\Omega }}}_{0}} + 2{{\omega }}}}{{R}^{{2n}}} - \frac{{{{\rho }}e{{{{\Omega }}}^{2}}}}{n}\frac{{{{{{\Omega }}}_{0}} - 2{{\omega }}}}{{{{{{\Omega }}}_{0}} + 2{{\omega }}}}{{R}^{{n + 1}}}{{{\text{e}}}^{{{\text{i(}}n - 1){{\theta }}}}}$На основании соотношений ${\text{i}}{{{{\Omega }}}_{0}}({{C}_{1}}{{r}^{n}} + {{C}_{2}}{{r}^{{--n}}}) = --{{\rho }}{{{{\omega }}}^{2}}rU(r)$, (3.6) и (3.7) получается, что
(3.8)
${{C}_{1}} = \frac{{{{\rho }}e{{{{\Omega }}}^{2}}}}{n}\frac{{{{\Omega }}_{0}^{2} - 2{{\omega }}{{{{\Omega }}}_{0}} - {{\bar {\bar {\sigma }}}}n{{{{\omega }}}^{2}}}}{{{{\Omega }}_{0}^{2} - 2{{\bar {\sigma }\omega }}{{{{\Omega }}}_{0}} - {{\bar {\sigma }}}n{{{{\omega }}}^{2}}}}\frac{{{{R}^{{n + 1}}}}}{{{{R}^{{2n}}} + {{r}^{{2n}}}}}{{{\text{e}}}^{{{\text{i(}}n - 1){{\theta }}}}}$Константа (3.7) при подстановке (3.8) преобразуется в:
(3.9)
${{C}_{2}} = - \frac{{{{\rho }}e{{{{\Omega }}}^{2}}}}{n}\frac{{{{{{\Omega }}}_{0}} - 2{{\omega }}}}{{{{{{\Omega }}}_{0}} + 2{{\omega }}}}\frac{{{{{{\Omega }}}_{0}}\left( {{{{{\Omega }}}_{0}} + 2{{\omega }}} \right){{r}^{{2n}}} + {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\bar {\sigma }} }}n{{{{\omega }}}^{2}}}}{{{{\Omega }}_{0}^{2} - 2{{\bar {\sigma }\omega }}{{{{\Omega }}}_{0}} - {{\bar {\sigma }}}n{{{{\omega }}}^{2}}}}\frac{{{{R}^{{n + 1}}}}}{{{{R}^{{2n}}} + {{r}^{{2n}}}}}{{{\text{e}}}^{{{\text{i(}}n - 1){{\theta }}}}}$Выражение (3.5) с заменами (3.8) и (3.9) принимает вид:
Соответственно
Таким образом, составляющие искомой гидродинамической силы согласно (2.2):
Для завершения формулировки, учитывая равенство ${{{{\Omega }}}_{0}} = {{\Omega }} - {{\omega }}$, остается лишь подставить выражение  в (3.1):
в (3.1):
(3.10)
$\begin{array}{*{20}{c}} {ke - me{{{{\Omega }}}^{2}} + {\text{i}}be\left( {{{\Omega }} - {{\omega }}} \right) + {\text{i}}de{{\Omega }} = \frac{{{{m}_{F}}e{{{{\Omega }}}^{2}}}}{n}f(R,r,n,{{\Omega }},{{\omega }})} \\ {f(R,r,n,{{\Omega }},{{\omega }}) = \frac{{{{\bar {\sigma }}}({{{{\Omega }}}^{2}} - 4{{\omega \Omega }} + 3{{{{\omega }}}^{2}}) - \left( {\frac{{1 - {{{{\chi }}}^{{n + 1}}}}}{{1 + {{{{\chi }}}^{{2n}}}}} + \frac{{{{{{\chi }}}^{{2n}}} - {{{{\chi }}}^{{n + 1}}}}}{{1 + {{{{\chi }}}^{{2n}}}}}\frac{{{{\Omega }} - 3{{\omega }}}}{{{{\Omega }} + {{\omega }}}}} \right)n{{{{\omega }}}^{2}}}}{{{{{{\Omega }}}^{2}} - 2\left( {1 + {{\bar {\sigma }}}} \right){{\omega \Omega }} + \left( {1 + 2{{\bar {\sigma }}} - {{\bar {\sigma }}}n} \right){{{{\omega }}}^{2}}}}} \end{array}$4. Анализ движения и устойчивости системы “ротор–жидкость”. Любая роторная система динамически устойчива, если ReΩ > 0 и ImΩ > 0 или ReΩ < 0 и ImΩ < 0. Принимая во внимание, что на границе динамической устойчивости, а также без учета диссипативных и неконсервативных сил ReΩ = Ω и ImΩ = 0, т.е. записывая порознь мнимую и вещественную части уравнения (3.10), можно получить два уравнения:
(4.1)
${{\omega }}_{0}^{2} - {{{{\Omega }}}^{2}} = \frac{{{{\mu }}{{{{\Omega }}}^{2}}}}{n}\frac{{{{\bar {\sigma }}}({{{{\Omega }}}^{2}} - 4{{\omega \Omega }} + 3{{{{\omega }}}^{2}}) - \left( {\frac{{1 - {{{{\chi }}}^{{n + 1}}}}}{{1 + {{{{\chi }}}^{{2n}}}}} + \frac{{{{{{\chi }}}^{{2n}}} - {{{{\chi }}}^{{n + 1}}}}}{{1 + {{{{\chi }}}^{{2n}}}}}\frac{{{{\Omega }} - 3{{\omega }}}}{{{{\Omega }} + {{\omega }}}}} \right)n{{{{\omega }}}^{2}}}}{{{{{{\Omega }}}^{2}} - 2\left( {1 + {{\bar {\sigma }}}} \right){{\omega \Omega }} + \left( {1 + 2{{\bar {\sigma }}} - {{\bar {\sigma }}}n} \right){{{{\omega }}}^{2}}}}$Первое уравнение определяет границу динамической устойчивости, т.е. критическое соотношение между скоростями ω и Ω, под действием учитываемых сил вязкого внутреннего и внешнего трения:
В более типичном для практики невязком случае гистерезисного внутреннего и внешнего трения [17]:
Отсюда в зависимости от скоростей прецессии и вращения могут быть три ситуации. В
двух из них: при прямой прецессии ${{{\Omega }} \mathord{\left/ {\vphantom {{{\Omega }} {\left| {{\Omega }} \right|}}} \right. \kern-0em} {\left| {{\Omega }} \right|}} = 1$ и скорости вращения меньше скорости прецессии  , а также при обратной прецессии ${{{\Omega }} \mathord{\left/ {\vphantom {{{\Omega }} {\left| {{\Omega }} \right|}}} \right. \kern-0em} {\left| {{\Omega }} \right|}} = - 1$ и любой скорости вращения
, а также при обратной прецессии ${{{\Omega }} \mathord{\left/ {\vphantom {{{\Omega }} {\left| {{\Omega }} \right|}}} \right. \kern-0em} {\left| {{\Omega }} \right|}} = - 1$ и любой скорости вращения  , система устойчива, так как ${{\eta }} + {{{{\eta }}}_{e}} \ne {\text{0}}$. Однако в третьей: при прямой прецессии ${{{\Omega }} \mathord{\left/ {\vphantom {{{\Omega }} {\left| {{\Omega }} \right|}}} \right. \kern-0em} {\left| {{\Omega }} \right|}} = 1$ и скорости вращения больше скорости прецессии
, система устойчива, так как ${{\eta }} + {{{{\eta }}}_{e}} \ne {\text{0}}$. Однако в третьей: при прямой прецессии ${{{\Omega }} \mathord{\left/ {\vphantom {{{\Omega }} {\left| {{\Omega }} \right|}}} \right. \kern-0em} {\left| {{\Omega }} \right|}} = 1$ и скорости вращения больше скорости прецессии  , система не всегда устойчива, а именно при ${{{{\eta }}}_{e}} \leqslant {{\eta }}$.
, система не всегда устойчива, а именно при ${{{{\eta }}}_{e}} \leqslant {{\eta }}$.
Второе уравнение определяет частоты самовозбуждающихся колебаний неконсервативной роторной системы вблизи границы динамической устойчивости или собственные частоты консервативной роторной системы в зависимости от скорости вращения.
В частности, при синхронном движении из (4.1):
(4.2)
${{\omega }} = {{\Omega }} = \frac{1}{{\sqrt {1 + {{{\mu }} \mathord{\left/ {\vphantom {{{\mu }} n}} \right. \kern-0em} n}} }}{{{{\omega }}}_{0}}$В общем асинхронном случае уравнение (4.1) сводится к многочлену вида:
(4.3)
$\begin{gathered} \left( {1 + {{\mu }}\frac{{{{\bar {\sigma }}}}}{n}} \right){{{{{\bar {\Omega }}}}}^{5}} - \left( {1 + 2{{\bar {\sigma }}} + 3{{\mu }}\frac{{{{\bar {\sigma }}}}}{n}} \right){{\bar {\omega }}}{{{{{\bar {\Omega }}}}}^{4}} - \\ - \;\left[ {1 + \left( {1 + {{\bar {\sigma }}}n + {{\mu }}\frac{{{{\bar {\sigma }}}}}{n} + {{\mu }}\frac{{1 + {{{{\chi }}}^{{2n}}} - 2{{{{\chi }}}^{{n + 1}}}}}{{1 + {{{{\chi }}}^{{2n}}}}}} \right){{{{{\bar {\omega }}}}}^{2}}} \right]{{{{{\bar {\Omega }}}}}^{3}} + \\ + \;\left[ {1 + 2{{\bar {\sigma }}} + \left( {1 + 2{{\bar {\sigma }}} - {{\bar {\sigma }}}n + 3{{\mu }}\frac{{{{\bar {\sigma }}}}}{n} - {{\mu }}\frac{{1 - 3{{{{\chi }}}^{{2n}}} + 2{{{{\chi }}}^{{n + 1}}}}}{{1 + {{{{\chi }}}^{{2n}}}}}} \right){{{{{\bar {\omega }}}}}^{2}}} \right]{{\bar {\omega }}}{{{{{\bar {\Omega }}}}}^{2}} + \\ + \;\left( {1 + {{\bar {\sigma }}}n} \right){{{{{\bar {\omega }}}}}^{2}}{{\bar {\Omega }}} - \left( {1 + 2{{\bar {\sigma }}} - {{\bar {\sigma }}}n} \right){{{{{\bar {\omega }}}}}^{3}} = 0 \\ \end{gathered} $В еще одном частном случае, либо при наличии в полости одной радиальной перегородки, либо при отсутствии перегородок, т.е. при n = 1:
(4.4)
$\begin{gathered} \left( {1 + {{\mu \bar {\sigma }}}} \right){{{{{\bar {\Omega }}}}}^{5}} - \left( {1 + 2{{\bar {\sigma }}} + 3{{\mu \bar {\sigma }}}} \right){{\bar {\omega }}}{{{{{\bar {\Omega }}}}}^{4}} - [1 + \left( {1 + {{\bar {\sigma }}} + 2{{\mu \bar {\sigma }}}} \right){{{{{\bar {\omega }}}}}^{2}}]{{{{{\bar {\Omega }}}}}^{3}} + \\ + \;[1 + 2{{\bar {\sigma }}} + \left( {1 + {{\bar {\sigma }}} + 2{{\mu \bar {\sigma }}}} \right){{{{{\bar {\omega }}}}}^{2}}]{{\bar {\omega }}}{{{{{\bar {\Omega }}}}}^{2}} + \left( {1 + {{\bar {\sigma }}}} \right){{{{{\bar {\omega }}}}}^{2}}{{\bar {\Omega }}} - \left( {1 + {{\bar {\sigma }}}} \right){{{{{\bar {\omega }}}}}^{3}} = 0 \\ \end{gathered} $В действительности, без перегородок уравнение (4.1) принимает особую форму:
(4.5)
$\begin{gathered} \left( {1 + {{\mu \bar {\sigma }}}} \right){{{{{\bar {\Omega }}}}}^{4}} - 2\left( {1 + 2{{\mu \bar {\sigma }}} + {{\bar {\sigma }}}} \right){{\bar {\omega }}}{{{{{\bar {\Omega }}}}}^{3}} - \\ - \;[1 - \left( {1 + 2{{\mu \bar {\sigma }}} + {{\bar {\sigma }}}} \right){{{{{\bar {\omega }}}}}^{2}}]{{{{{\bar {\Omega }}}}}^{2}} + 2\left( {1 + {{\bar {\sigma }}}} \right){{\bar {\omega }\bar {\Omega }}} - \left( {1 + {{\bar {\sigma }}}} \right){{{{{\bar {\omega }}}}}^{2}} = 0 \\ \end{gathered} $Математическое снижение размерности на единицу физически означает удаление из системы одной частоты собственных колебаний, а именно связанной с жидкостью. Ее возмущенное окружное течение при пульсирующе неравномерном вращении в неразделенной и даже однажды перегороженной полости принципиально различно. Это понятно из механической аналогии, если представить скорости циркулирующей внутри полости жидкости как касательные напряжения, распределяющиеся при кручении в трубе замкнутого и незамкнутого сечения (рис. 3). В замкнутом тонкостенном профиле касательные напряжения распределяются по толщине почти равномерно; в открытом (незамкнутом) профиле распределение происходит по линейному закону, причем на средней линии сечения касательные напряжения обращаются в нуль.
Рис. 3.
Схема потоков касательных напряжений в замкнутом и открытом профиле трубы или жидкости в неравномерно вращающейся неразделенной и один раз перегороженной полости.

Полином 4-й степени имеет необозримо громоздкое общее решение, а полином 5-й степени уже даже не поддается аналитическому решению. Численно рассчитанные результаты удобнее всего представить в виде графика зависимости возможных скоростей прецессии от скорости вращения ротора.
На рис. 4 приведены результаты по (4.5) и (4.4) для реальной системы “ротор–жидкость” (табл. 1) без перегородок (рис. 4, a) и с одной радиальной перегородкой (рис. 4, b) в роторной полости (n = 1, ${{\bar {\sigma }}}$ = 0.34). Для этой же системы также показаны результаты по (4.3) в случаях с двумя (n = 2, ${{\bar {\sigma }}}$ = 0.61, рис. 4, c) и тремя (n = 3, ${{\bar {\sigma }}}$ = 0.79, рис. 4, d) радиальными перегородками в роторе.
Рис. 4.
Диаграмма частот системы “ротор-жидкость” без перегородок (а), с одной (b), двумя (с) и тремя (d) радиальными перегородками.

Таблица 1.
Исходные характеристики реальной роторной системы
| Параметр | Обозначение | Значение | Размерность |
|---|---|---|---|
| Масса пустого ротора | m | 0.24 | кг |
| Критическая частота пустого ротора | ω0/(2π) | 50 | Гц |
| Критическая частота полного (жидкостью) ротора | 1/(2π)${{\omega }_{0}}{\text{/}}\sqrt {1 + \mu } $ | 41 | Гц |
| Радиус роторной полости | R | 31.5 | мм |
| Длина роторной полости | L | 34 | мм |
| Отношение массы жидкости (заполняющей всю роторную полость) к массе пустого ротора | µ = mF/m | ≈0.5 | – |
| Отношение радиуса свободной поверхности вращающейся жидкости к радиусу роторной полости | χ = $\frac{r}{R}$ | ≈0.7* | – |
Как видно, все диаграммы частот значительно отличаются друг от друга. На первой из представленных диаграмм для каждого значения скорости вращения ${{\bar {\omega }}}$ существуют четыре значения ${{\bar {\Omega }}}$, на остальных – для каждой ${{\bar {\omega }}}$ – пять прецессионных скоростей ${{\bar {\Omega }}}$. На рис. 4 присутствует известное пересечение линии Ω = ω с графиком одной из частот (т. С), которая определяет критическую скорость роторной системы. Легко может быть проверено, что точка С равна значению, следующему из формулы (4.2), т.е. совпадает с критической скоростью полного (жидкостью) ротора.
Число значений ${{\bar {\Omega }}}$ сохраняется и в интервалах скоростей ротора, отмеченных пунктиром. Вне таких интервалов
решения (полиномов) содержат только положительные и отрицательные вещественные корни,
однако внутри них решения дают также комплексно-сопряженные корни, и, конечно, некоторые
из них имеют мнимую часть с противоположным знаком к действительной. Если такие корни
подставить в экспоненциальную функцию  , то получится нарастание амплитуды или неустойчивое прецессионное движение. Другими
словами, определены диапазоны самовозбуждающихся неустойчивых прецессий, совершающихся
с той или иной собственной частотой системы. Здесь следует подчеркнуть, что вычисленные
${{\bar {\Omega }}}$ – это круговые собственные частоты системы “колеблющийся ротор–колеблющаяся в нем
жидкость”.
, то получится нарастание амплитуды или неустойчивое прецессионное движение. Другими
словами, определены диапазоны самовозбуждающихся неустойчивых прецессий, совершающихся
с той или иной собственной частотой системы. Здесь следует подчеркнуть, что вычисленные
${{\bar {\Omega }}}$ – это круговые собственные частоты системы “колеблющийся ротор–колеблющаяся в нем
жидкость”.
Частоты собственных колебаний жидкости, вращающейся в жестком роторе на жестких подшипниках, определяются уравнением, также содержащимся в (4.1); а именно в знаменателе (4.1). В безразмерном случае оно имеет следующие вид и корни:
(4.6)
${{{{\bar {\Omega }}}}^{2}} - 2\left( {1 + {{\bar {\sigma }}}} \right){{\bar {\omega }\bar {\Omega }}} + \left( {1 + 2{{\bar {\sigma }}} - {{\bar {\sigma }}}n} \right){{{{\bar {\omega }}}}^{2}} = 0$Здесь нижним знаком характеризуется волна, распространяющаяся против вращения, а верхним – прямая волна, поскольку уравнение (4.6) не что иное как частный случай известного уравнения физических частот Ωk свободных плоских волн на поверхности вращающейся жидкости [18]:
Для сравнения графики зависимости соответствующих частот ${{{{\bar {\Omega }}}}_{{1,2}}}$ от ${{\bar {\omega }}}$ при n = 1 наложены на частотную диаграмму системы “колеблющийся ротор – колеблющаяся в его полости с одной перегородкой жидкость” (рис. 5).
Рис. 5.
Диаграмма волновых частот Ω1,2 вращающейся жидкости и собственных частот системы “ротор–жидкость” при n = 1.

Очевидно, в системе две собственные частоты из пяти вызваны прямым и обратным волновым движением жидкости ${{{{\Omega }}}_{{1,2}}} \simeq \pm {{{{\Omega }}}_{k}}$, еще две другие обусловлены прямым и обратным прецессионным движением ротора ${{{{\Omega }}}_{{3,4}}} \simeq \pm E{{{{\omega }}}_{0}}$, где $E \in [{1 \mathord{\left/ {\vphantom {1 {\sqrt {1 + {{{\mu }} \mathord{\left/ {\vphantom {{{\mu }} n}} \right. \kern-0em} n}} }}} \right. \kern-0em} {\sqrt {1 + {{{\mu }} \mathord{\left/ {\vphantom {{{\mu }} n}} \right. \kern-0em} n}} }}\; \ldots \;1]$. Что касается пятой собственной частоты, по-видимому, ${{{{\Omega }}}_{5}}$ связана с –ω или с обратным и в то же время синхронизированным с вращением течением жидкости в перегороженной полости по типу отмеченной выше механической аналогии (рис. 3).
5. Заключение. Таким образом, определены диапазоны динамической неустойчивости ротора при неполном наливе жидкости и равномерной постановке малого количества радиальных перегородок внутрь него. Дестабилизирующее влияние жидкости проявляется на закритических оборотах и оказывается неожиданно большим в случае двух радиальных перегородок, несмотря на то, что делят роторную полость пополам и образуют геометрически уравновешенную конфигурацию системы.
Список литературы
Selmi M., Herbert T. Resonance phenomena in viscous fluids inside partially filled spinning and nutating cylinders // Phys. Fluids. 1995. V. 7. № 108. P. 108–120. https://doi.org/10.1063/1.868731
Ulbrich H., Cyllik A., Ahaus G. Stabilization of centrifuges with instabilities due to fluid – structure interactions: Various control approaches // Int. J. Rotat. Mach. 2001. V. 7. № 5. P. 323–333, https://doi.org/10.1155/S1023621X01000276
Soto-Urbiola L., Lopez-Parra M. Liquid self-balancing device effects on flexible rotor stability // Shock Vibr. 2013. V. 20. P. 109–121, https://doi.org/10.3233/SAV-2012-0731
Marques F., Lopez J.M. Precession of a rapidly rotating cylinder flow: traverse through resonance // J. Fluid Mech. 2015. V. 782. P. 63–98, https://doi.org/10.1017/jfm.2015.524
Preussner C., Kollmann F.G. On the stability of a spinning, fluid filled and sectored rotor // Comp. Struct. 1988. V. 30. № 1–2. P. 131–141, https://doi.org/10.1016/0045-7949(88)90221-0
Tao M., Zhang W. Dynamic stability of a rotor partially filled with a viscous liquid // J. Appl. Mech., Trans. ASME. 2002. V. 69. № 5. P. 705–707, https://doi.org/10.1115/1.1458553
Дерендяев Н.В. Устойчивость вращения роторных систем, содержащих жидкость. Нижний Новгород: Изд-во ННГУ, 2014. 154 с.
Ishida Y., Liu J. Elimination of unstable ranges of rotors utilizing discontinuous spring characteristics: an asymmetrical shaft system, an asymmetrical rotor system, and a rotor system with liquid // ASME J. Vibr. Acoust. 2010. V. 132. № 1. P. 011011, https://doi.org/10.1115/1.4000842
Firouz-Abadi R.D., Permoon M.R., Haddadpour H. On the instability of spinning cylindrical shells partially filled with liquid // Int. J. Struct. Stab. Dyn. 2012. V. 12. № 3. P. 1250018, https://doi.org/10.1142/S0219455412500186
Kern D., Jehle G. Dynamics of a rotor partially filled with viscous incompressible fluid // Proc. Appl. Math. Mech. 2016. V. 16. P. 279–280, https://doi.org/10.1002/pamm.201610128
Dyakova V., Kozlov V., Polezhaev D. Oscillation-induced sand dunes in a liquid-filled rotating cylinder // Phys. Rev. E. 2016. V. 94. P. 063109, https://doi.org/10.1103/PhysRevE.94.063109
Wang G., Yuan H. An analysis of dynamic stability for a flexible rotor filled with liquid // Phys. Fluids. 2018. V. 30. P. 037101, https://doi.org/10.1063/1.5017582
Wang H., Chen G., Jiang G. Stability analysis of an anisotropic rotor partially filled with viscous incompressible fluid based on Andronov-Hopf bifurcation // Phys. Fluids. 2021. V. 33. P. 064111, https://doi.org/10.1063/5.0055675
Хронин Д.В. Теория и расчет колебаний в двигателях летательных аппаратов. М.: Машиностроение, 1970. 412 с.
Гольдштик М.А., Штерн В.Н., Яворский Н.И. Вязкие течения с парадоксальными свойствами. Новосибирск: Наука (сибирское отделение), 1989. 336 с.
Firouz-Abadi R.D., Haddadpour H. The flexural instability of spinning flexible cylinder partially filled with viscous liquid // J. Appl. Mech. 2010. V. 77. № 1. P. 011001, https://doi.org/10.1115/1.3172143
Голоскоков Е.Г., Филиппов А.П. Нестационарные колебания механических систем. Киев: Наукова думка, 1966. 336 с.
Nikiforov A. Natural surface oscillations of rotating fluid along radial baffles of rotor // ASME J. Fluids Eng. 2016. V. 138. № 6. P. 061202, https://doi.org/10.1115/1.4032300
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела