1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2022

Известия РАН. Механика твердого тела, 2022, № 3, стр. 88-96

ВЛИЯНИЕ ДАВЛЕНИЯ ОКРУЖАЮЩЕЙ СРЕДЫ НА НИЗШУЮ ЧАСТОТУ КОЛЕБАНИЙ ПЛАСТИНЫ

М. А. Ильгамов a, b, c, *, А. Г. Хакимов a, **

a Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия

b Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

c Башкирский государственный университет
Уфа, Россия

* E-mail: ilgamov@anrb.ru
** E-mail: hakimov@anrb.ru

Поступила в редакцию 15.03.2021
После доработки 11.09.2021
Принята к публикации 12.10.2021

Полный текст (PDF)

Аннотация

Определяется низшая частота изгибных колебаний пластины, контактирующей с жидкостью или газом. Дается вывод выражения распределенной поперечной нагрузки на пластину в предположении ее цилиндрического изгиба. Поверхности пластины контактируют со средой разной плотности и давления. Среда может быть сжимаемой в процессе деформации поверхности и несжимаемой. Определяется влияние на изгиб взаимодействия среднего давления и изменения кривизны срединной поверхности, а также присоединенной массы газовой среды.

Ключевые слова: тонкая пластина, жидкость, газ, плотность, давление, присоединенная масса

1. Введение. Определение спектра частот пластин и оболочек, контактирующих с жидкостью и газом, имеет большое значение [1–3]. Этой теме посвящена обширная литература. К ней примыкает также серия работ по колебаниям тонкостенных тел, не контактирующих с внешней средой.

Работа [4] посвящена аналитическому решению для определения собственных частот и форм изгибных колебаний защемленной по контуру квадратной однородной пластины. Произведено также сравнение расчетов с экспериментальными данными. Предложенная методика исследований и алгоритм расчета могут быть использованы для исследования изгибных колебаний пластин при других типах граничных условий. В [5] рассматривается задача расчета ортотропных полигональных пластин, подвергающихся акустическому воздействию с широким спектром.

В последнее время динамическая теория пластин находит широкое применение в анализе поведения упругих элементов микро- и наноразмеров. Среди многочисленных видов применения микро- и нанопленок, нанопроволок, нанотрубок может быть указано также использование их в качестве детекторов и сенсоров в химии, биологии и т.д [6–8]. Ввиду уникального применения изучению их эксплуатационных свойств уделяется в литературе большое внимание. Например, в [9, 10] дается обзор четырехсот статей, посвященных главным образом консольным резонаторам из нанопленок и нанопроволок. В [11] сообщалось о сверхчувствительных наномеханических резонаторах для структурных исследований ДНК-лигандных комплексов. Резонаторы с электростатическим приводом продемонстрировали большой потенциал в широком спектре применений, таких как датчики, устройства связи, логические элементы и квантовые измерения [12]. Для обнаружения и идентификации различных биочастиц и оценки их размеров в [13] применяется механический наносенсор. Решение нелинейного уравнения проводится с помощью метода Галеркина. В [14] анализируется динамическая неустойчивость консольной нанобалки, соединенной с горизонтальной пружиной.

Однако во всех этих работах взаимодействие среднего давления сред и разности площадей выпуклой и вогнутой поверхностей пластины не учитывается. Это взаимодействие принимается во внимание в [15, 16] в случае легких газов, когда присоединенная масса сред мала. В монографиях [1–3] также не учитывается указанный эффект среднего давления. В [17] определяется спектр частот двухопорного резонатора с учетом взаимодействия среднего избыточного давления на поверхности резонатора и кривизны, а также действия осевой нагрузки.

В данной работе определяется низшая собственная частота пластинки с учетом взаимодействия среднего избыточного давления на ее поверхности и кривизны срединной поверхности, а также действия присоединенной массы газовой среды с удаленными границами. В отличие от постановки задач в [1–3], где задается частота и определяется волновое число, здесь конструктивно задается длина полуволны и определяется частота. Такая постановка характерна для резонаторов.

Представляет интерес вопрос о взаимном влиянии эффекта среднего давления и известного из литературы эффекта присоединенной массы жидкости на деформацию пластины. Это проще выяснить в случае несжимаемой жидкости. Далее, с учетом полученного результата рассматривается случай сжимаемой жидкости в более простой постановке (в частности, не производится разложение в ряд Тейлора условий контакта).

В предположении цилиндрического изгиба тонкой пластины рассматривается уравнение [18]

(1.1)
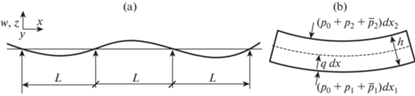
$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + {{\rho }}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = q,\quad D = \frac{{E{{h}^{3}}}}{{12(1 - {{{{\nu }}}^{2}})}}$
где E, ν, ρ – модуль упругости, коэффициент Пуассона, плотность материала, h – толщина пластины, w(x, t) – прогиб, х, t – координата, время, q – поперечная распределенная нагрузка.

На нижнюю и верхнюю поверхность пластины действуют давления р0 + р1 и р0 + р2 жидкостей с плотностями ρ1 и ρ2 (рис. 1, a). Здесь р0 – давление сборки, в частности, атмосферное давление, действующее на все поверхности, р1, р2 – избыточные давления. При определении нагрузки q исходим из предположения, что ρ1, ρ2 и р1, р2 остаются постоянными при изгибе пластины.

Рис. 1.

(a) Пример крепления пластины. (b) Элемент dx срединной поверхности изогнутой пластины.

2. Несжимаемая среда. Предполагаем, что области, занятые жидкостями, простираются неограниченно, опоры не препятствуют свободному перетеканию жидкости вдоль пластины в направлении оси x. Возникающие в результате движения пластины давления обозначим через ${{\bar {p}}_{1}}$ и ${{\bar {p}}_{2}}$. Уравнения динамики несжимаемой жидкости относительно потенциала скорости φ(x, z, t) имеют вид [1–3]

(2.1)
$\frac{{{{\partial }^{2}}{{{{\varphi }}}_{{1,2}}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{{{\varphi }}}_{{1,2}}}}}{{\partial {{z}^{2}}}} = 0,\quad {{\bar {p}}_{{1,2}}} = - {{{{\rho }}}_{{1,2}}}\frac{{\partial {{{{\varphi }}}_{{1,2}}}}}{{\partial t}}$

Условия на поверхностях

(2.2)
$\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} = \frac{{\partial w}}{{\partial t}}\left( {z = - \frac{h}{2} + w} \right),\quad \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} = \frac{{\partial w}}{{\partial t}}\left( {z = \frac{h}{2} + w} \right)$

На большом удалении от поверхности возмущения от пластины исчезают

(2.3)
$\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} = 0\left( {z = - \infty } \right),\quad \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} = 0\left( {z = \infty } \right)$

Элементарные длины dx1, dx2 нижней и верхней поверхностей, выраженные через длину dx срединной поверхности пластины, равны (рис. 1, b)

(2.4)
$d{{x}_{1}} = \left( {1 + {{\varepsilon }_{x}}\left( { - \frac{h}{2}} \right)} \right)dx,\quad d{{x}_{2}} = \left( {1 + {{\varepsilon }_{x}}\left( {\frac{h}{2}} \right)} \right)dx$
где деформации в соответствии с гипотезами Кирхгоффа [18]

(2.5)
${{\varepsilon }_{x}}\left( { - \frac{h}{2}} \right) = \frac{h}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}},\quad {{\varepsilon }_{x}}\left( {\frac{h}{2}} \right) = - \frac{h}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}$

Распределенная сила q определяется по формуле [15, 16]

(2.6)
$qdx = \left( {{{p}_{0}} + {{p}_{1}} + {{{\bar {p}}}_{1}}} \right)d{{x}_{1}} - \left( {{{p}_{0}} + {{p}_{2}} + {{{\bar {p}}}_{2}}} \right)d{{x}_{2}}$

Предполагаем, что пластина неограниченной длины по оси x опирается на опоры, расположенные на равных расстояниях L и допускающие свободный поворот. Примем

(2.7)
что удовлетворяет условиям w = 0, ∂2w/∂x2 = 0 при |x| = 0, L, 2L, … . Тогда в функциях
(2.8)
${{{{\varphi }}}_{1}} = {{\Phi }_{1}}\left( z \right)\sin {{\beta }}x\cos {{\omega }}t,\quad {{{{\varphi }}}_{2}} = {{\Phi }_{2}}\left( z \right)\sin {{\beta }}x\cos {{\omega }}t$
по (2.1) имеем ${{\Phi }_{1}}\left( z \right) = {{A}_{1}}\exp \left( {{{\beta }}z} \right),{{\Phi }_{2}}\left( z \right) = {{A}_{2}}\exp \left( { - {{\beta }}z} \right)$. При этом удовлетворяются условия (2.3).

Разлагая функции ∂φ1/∂z, ∂φ2/∂z в ряд Тейлора в окрестности z = 0, условия (2.2) приведем к виду

$\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} + \left( { - \frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial {{z}^{2}}}} = \frac{{\partial w}}{{\partial t}}\left( {z = 0} \right),\quad \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} + \left( {\frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial {{z}^{2}}}} = \frac{{\partial w}}{{\partial t}}\left( {z = 0} \right)$

В линейной задаче член с w в данных условиях должен быть опущен. Подставляя сюда выражения (2.7), (2.8) с учетом Φ1, Φ2, получаем

${{A}_{1}} = W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}},\quad {{A}_{2}} = - W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}}$

Выражения (2.8) через амплитуду прогиба W приобретают вид

(2.9)
${{{{\varphi }}}_{1}} = W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}}\exp \left( {{{\beta }}z} \right)\sin {{\beta }}x\cos {{\omega }}t$
${{{{\varphi }}}_{2}} = - W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}}\exp \left( { - {{\beta }}z} \right)\sin {{\beta }}x\cos {{\omega }}t$

При вычислении акустического давления на поверхностях пластины z = – h/2 + w, z = h/2 + w выражение (2.1) также сведем к поверхности z = 0

${{\bar {p}}_{1}} = - {{{{\rho }}}_{1}}\left[ {\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial t}} + \left( { - \frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial t\partial z}}} \right](z = 0)$
${{\bar {p}}_{2}} = - {{{{\rho }}}_{2}}\left[ {\frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial t}} + \left( {\frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial t\partial z}}} \right](z = 0)$

Подставим сюда выражения (2.9), предварительно опустив нелинейные члены с w. Тогда получаем

${{\bar {p}}_{1}} = W\frac{{{{{{\rho }}}_{1}}{{{{\omega }}}^{2}}}}{{{\beta }}}\sin {{\beta }}x\sin {{\omega }}t,\quad {{\bar {p}}_{2}} = - W\frac{{{{{{\rho }}}_{2}}{{{{\omega }}}^{2}}}}{{{\beta }}}\sin {{\beta }}x\sin {{\omega }}t$

С учетом соотношения для прогиба эти выражения могут быть представлены в виде

(2.10)
${{\bar {p}}_{1}} = - \frac{{{{{{\rho }}}_{1}}}}{{{\beta }}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}},\quad {{\bar {p}}_{2}} = \frac{{{{{{\rho }}}_{2}}}}{{{\beta }}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}$

Из (2.6), (2.4), (2.5), (2.10) находим распределенную поперечную нагрузку

(2.11)
$q = {{p}_{1}} - {{p}_{2}} + \frac{{\left( {2{{p}_{0}} + {{p}_{1}} + {{p}_{2}}} \right)h}}{2} \cdot \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - \frac{{{{{{\rho }}}_{1}} + {{{{\rho }}}_{2}}}}{{{\beta }}} \cdot \frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + \left[ { - \frac{{{{{{\rho }}}_{1}} - {{{{\rho }}}_{2}}}}{{{\beta }}} \cdot \frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}} \right]\frac{h}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}$

Последний член в скобках (2.11) должен быть опущен в рамках принятого приближения линейной теории. Он обращается в нуль при ρ1 = ρ2.

Уравнение (1.1) с учетом (2.11)

(2.12)
$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} - \frac{{\left( {2{{p}_{0}} + {{p}_{1}} + {{p}_{2}}} \right)h}}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \left( {{{\rho }}h + \frac{{{{{{\rho }}}_{1}} + {{{{\rho }}}_{2}}}}{{{\beta }}}} \right)\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = {{p}_{1}} - {{p}_{2}}$

В частном случае ρ1 = ρ2, p1 = p2 и функции прогиба (2.7) из (2.12) получаем для низшей собственной частоты ω

(2.13)
${{{{\omega }}}^{2}} = {{\omega }}_{0}^{2}\frac{{1 + {{\alpha }}}}{{1 + {{\mu }}}},\quad {{\omega }}_{0}^{2} = \frac{{D{{{{\beta }}}^{4}}}}{{{{\rho }}h}},\quad {{\alpha }} = \frac{{\left( {{{p}_{0}} + {{p}_{1}}} \right)h}}{{D{{{{\beta }}}^{2}}}},\quad {{\mu }} = \frac{{2{{{{\rho }}}_{1}}}}{{{{\rho }}h{{\beta }}}}$

Здесь ω0 – частота пластины, не контактирующей с жидкостью. Параметры α и μ определяют влияние давления и плотности окружающей среды. Таким образом, давление повышает, плотность понижает собственную частоту пластины. При α ≪ 1, μ ≪ 1 их влияние исчезает. Через исходные параметры α, μ записываются

(2.14)
${{\alpha }} \approx \frac{{{{p}_{0}} + {{p}_{1}}}}{E}{{\left( {\frac{L}{h}} \right)}^{2}},\quad {{\mu }} = \frac{{2{{{{\rho }}}_{1}}L}}{{{{\pi \rho }}h}}$

При E = 2 × 105 МПа, ν = 0.3, ρ = 7.8 × 103 кг/м3, ρ1 = 103 кг/м3, p0 = 0, p1 = 2 МПа, L/h = 1, α ≈ 10–3, μ = 0.81. Следовательно, нет влияния давления, имеется значительное снижение собственной частоты за счет присоединенной массы.

Если p1 = 20 МПа, L/h = 100, то $\alpha \approx {{10}^{{ - 4}}} \times {{10}^{4}} \approx 1$, μ = 8.1. По модели несжимаемой жидкости в случае воды имеется только снижение собственной частоты. Это известный результат [1–3], однако учет влияния давления вносит некоторое изменение частоты.

Общая оценка рассматриваемых эффектов состоит в том, что при α > μ преобладает повышающее частоту влияние давления среды, а при α < μ – понижающее влияние плотности (или присоединенной массы). Через входные параметры эти неравенства имеют вид

$\frac{{{{p}_{1}}\rho L}}{{E{{\rho }_{1}}h}} > 1,\quad \frac{{{{p}_{1}}\rho L}}{{E{{\rho }_{1}}h}} < 1$

Первый случай реализуется для весьма тонких пластин из материала с малым модулем упругости и при предельно высоком давлении в контактирующей среде. Второй случай всегда реализуется при невысоких давлениях в плотной среде.

3. Сжимаемая среда. По модели сжимаемой среды вместо уравнений (2.1) имеем [1–3]

(3.1)
$\frac{{{{\partial }^{2}}{{\varphi }_{{1,2}}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{{1,2}}}}}{{\partial {{z}^{2}}}} - \frac{1}{{c_{{1,2}}^{2}}} \cdot \frac{{{{\partial }^{2}}{{\varphi }_{{1,2}}}}}{{\partial {{t}^{2}}}} = 0,\quad {{\bar {p}}_{{1,2}}} = - {{\rho }_{{1,2}}}\frac{{\partial {{\varphi }_{{1,2}}}}}{{\partial t}},\quad c_{{1,2}}^{2} = {{\kappa }_{{1,2}}}\frac{{{{p}_{{1,2}}}}}{{{{\rho }_{{1,2}}}}}$
где, ${{с}_{{1,2}}}$ – скорость звука,${{\kappa }_{{1,2}}}$ – коэффициент адиабаты. В отличие от случая несжимаемой жидкости здесь давление и плотность не являются независимыми, а связаны изотермическим законом.

Рассмотрим частный случай одинаковых сред при одинаковых давлениях (ρ1 = ρ2, p1 = p2, c1 = c2). При функциях (2.7), (2.8)

(3.2)
$w = W\sin \beta x\sin \omega t,\quad {{\varphi }_{{1,2}}} = {{\Phi }_{{1,2}}}\left( z \right)\sin \beta x\cos \omega t$
из волнового уравнения (3.1) следует

(3.3)
${{\Phi }_{{1,2}}} = {{A}_{{1,2}}}{{e}^{{kz}}} + {{B}_{{1,2}}}{{e}^{{ - kz}}},\quad {{k}^{2}} = {{\beta }^{2}} - \frac{{{{\omega }^{2}}}}{{c_{1}^{2}}}$

Будем рассматривать случай k2 > 0. Обоснование этого условия приводится далее. Положив A2 = 0, B1 = 0 в соответствии с условиями (2.3), получаем частное решение

(3.4)
${{\varphi }_{1}} = {{A}_{1}}{{e}^{{kz}}}{\text{sin}}\beta x\cos \omega t,\,\,\,\,\,{{\varphi }_{2}} = {{B}_{2}}{{e}^{{ - kz}}}{\text{sin}}\beta x\cos \omega t$

Как показано выше, при определении распределенной нагрузки q необходимо учитывать условия при z = ±h/2, а при определении ${{\bar {p}}_{1}}$, ${{\bar {p}}_{2}}$ на поверхностях пластины и удовлетворении условий (3.2) в линейной задаче вместо z = ±h/2 + w можно принять z = 0. Тогда из условий (3.4) A1 = ωW/k, B2 = – ωW/k и

${{\bar {p}}_{1}} = - {{{{\rho }}}_{1}}\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial t}} = {{{{\rho }}}_{1}}\frac{{{{{{\omega }}}^{2}}}}{k}W\sin {{\beta }}x\sin \omega t,\quad {{\bar {p}}_{2}} = - {{{{\rho }}}_{2}}\frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial t}} = - {{{{\rho }}}_{2}}\frac{{{{{{\omega }}}^{2}}}}{k}W\sin {{\beta }}x\sin \omega t$

Правая часть уравнения (1.1) равна (ρ1 = ρ2, p1 = p2)

(3.5)
$q = \left( {{{p}_{0}} + {{p}_{1}}} \right)h\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{\bar {p}}_{1}} - {{\bar {p}}_{2}} = {{p}_{1}}h\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{{2{{{{\rho }}}_{1}}{{{{\omega }}}^{2}}}}{k}W\sin \beta x\sin \omega t$

Подставив в (1.1) выражение w и q из (3.2) и (3.5), получим для p0 = 0

(3.6)
$\begin{gathered} D{{\beta }^{4}} - \rho h{{{{\omega }}}^{2}} + {{p}_{1}}h{{{{\beta }}}^{2}} - \frac{{2{{{{\rho }}}_{1}}{{{{\omega }}}^{2}}}}{k} = 0 \\ {{\omega }}_{0}^{2} = \frac{{D{{\beta }^{4}}}}{{\rho h}},\quad {{k}^{2}} = {{\beta }^{2}} - \frac{{{{\omega }^{2}}}}{{c_{1}^{2}}},\quad {{\beta }} = \frac{\pi }{L} \\ \end{gathered} $

Из (3.6) следует

(3.7)
${\text{1}} - Z + \alpha - \frac{{\mu Z}}{{\sqrt {1 - \eta {\text{Z}}} }} = 0,\quad \alpha = \frac{{{{p}_{1}}{{\beta }^{2}}}}{{\rho {{\omega }}_{0}^{2}}},\quad {{\mu }} = \frac{{2{{{{\rho }}}_{1}}}}{{{{\rho }}h{{\beta }}}},\quad \eta = \frac{{{{\omega }}_{0}^{2}}}{{c_{1}^{2}{{\beta }^{2}}}},\quad Z = \frac{{{{\omega }^{2}}}}{{\omega _{0}^{2}}}$

Рассмотрим случай $1 - \eta {\text{Z}} > 0$. Частотное уравнение (3.7) представим в виде кубического

(3.8)
$\begin{gathered} {{Z}^{3}} + {{b}_{1}}{{Z}^{2}} + {{b}_{2}}Z - {{b}_{3}} = 0 \\ {{b}_{1}} = - 2\delta - \frac{1}{\eta } + \frac{{{{\mu }^{2}}}}{\eta },\quad {{b}_{2}} = {{\delta }^{2}} + \frac{{2\delta }}{\eta },\quad {{b}_{3}} = - \frac{{{{\delta }^{2}}}}{\eta },\quad \delta = 1 + \alpha \\ \end{gathered} $

Низшая собственная частота колебаний равна ${{f}_{1}} = {\omega \mathord{\left/ {\vphantom {\omega {2\pi ,\quad }}} \right. \kern-0em} {2\pi ,\quad }}\omega = {{\omega }_{0}}\sqrt Z .$

При E = 76 × 103 МПа, ν = 037, ρ = 10500 кг/м3, h = 20 нм, L = 2000 нм, ${{\kappa }_{{1,2}}}$ = 1.4, атмосферном давлении pa = 0.1 МПа, плотности воздуха ρ1a = 1.2928 кг/м3, p1 = 2 МПа численное решение уравнения (3.7) дает корень: Z = 1.10268. Соответствующая частота равна f1 = 6.894 МГц. Решение кубического уравнения (3.8), естественно, дает такой же корень: Z = 1.10268.

Для проверки выполнения условия k2 > 0 учтем полученное выражение $\omega = {{\omega }_{0}}\sqrt Z $, где ω0 дается в (3.6). В рассмотренном примере Z ≈ 1.1, т.е. имеет место преобладание влияния давления воздуха над его плотностью. Условие k2 > 0 или

${{\left( {\frac{c}{{{{c}_{1}}}}} \right)}^{2}}{{\left( {\frac{h}{L}} \right)}^{2}} < 10,\quad {{c}^{2}} = \frac{E}{{(1 - {{\nu }^{2}}){{\rho }}}}$
при L/h > 10 для случая стальной пластины и воды выполняется всегда, а в случае газов – при больших значениях L/h (например, L/h > 15).

Приведем приближенное решение уравнения (3.7). Примем Z = 1 – a, a3 ≪ 1. Подставим это выражение в (3.7) и приравняем нулю, пренебрегая членом, содержащим a3,

(3.9)
$\begin{gathered} {{d}_{1}}{{a}^{2}} + {{d}_{2}}a + {{d}_{3}} = 0,\quad {{d}_{1}} = 2\delta \eta - 3\eta + 1 - {{\mu }^{2}} \\ {{d}_{2}} = ({{\delta }^{2}} - 4\delta + 3)\eta + 2{{\mu }^{2}} + 2\delta - 2,\quad {{d}_{3}} = {{\left( {1 - \delta } \right)}^{2}}\left( {1 + \eta } \right) - {{\mu }^{2}} \\ \end{gathered} $

Из (3.9) находим

$a = \frac{{ - {{d}_{2}} + \sqrt {d_{2}^{2} - 4{{d}_{1}}{{d}_{3}}} }}{{2{{d}_{1}}}}$

Если δ = 1, то d1 = 1 – η – η2, d2 = 2µ2, d3 = – µ2.

Если пренебречь членом, содержащим a2, то получим a = –d3/d2.

Результаты расчета низшей собственной частоты изгибных колебаний пластинки по приближенным формулам (3.9) и a = –d3/d2 в соответствии с условиями на величину a сведены в табл. Для воздуха в рассматриваемом диапазоне давлений формула a = –d3/d2 дает погрешность не более 9%.

Также приведем решение уравнения (3.7) в виде

(3.10)
$Z = \frac{\delta }{{1 + {{\mu }}}}[{{C}_{1}} + {{С}_{2}}\eta \mu \delta + {{С}_{3}}{{\eta }^{2}}\mu {{\delta }^{2}}]$

Для η ≪ 1 представим $\sqrt {1 - \eta {\text{Z}}} $ как

(3.11)
$\sqrt {1 - \eta {\text{Z}}} \approx 1 - \frac{1}{2}\eta Z \approx \frac{1}{2}\frac{{\eta \delta \left( {{{C}_{1}} + {{C}_{1}}\mu + {{C}_{2}}\delta } \right)}}{{{{{\left( {1 + \mu } \right)}}^{2}}}}$

Подставляя выражения (3.10), (3.11) в уравнение (3.7), разлагая полученное соотношение в ряд по степеням δ и приравнивая нулю коэффициенты при δ, δ2, δ3, получим систему трех линейных уравнений, решение которой записывается

${{С}_{1}} = 1,\quad {{С}_{2}} = - \frac{1}{{2{{{\left( {1 + {{\mu }}} \right)}}^{2}}}},\quad {{С}_{3}} = - \frac{{1 - \mu }}{{4{{{\left( {1 + {{\mu }}} \right)}}^{4}}}}$

Из приведенных расчетов видно, что внешнее давление и наличие газа оказывает существенное влияние на частоты колебаний пластины. Также отметим высокую точность приближенной формулы (3.9) и решения в виде (3.10).

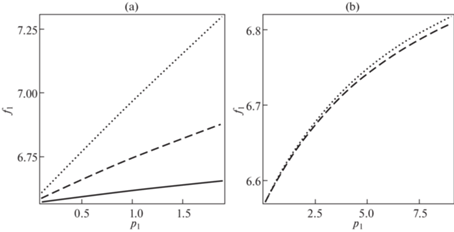
На рис. 2, а приводится зависимость первой частоты изгибных колебаний пластинки от давления для разных газов. Из рис. 2, а видно, что с ростом давления собственная частота колебаний возрастает. А с увеличением плотности газа происходит уменьшение собственной частоты изгибных колебаний. На рис. 2, b приводится зависимость первой частоты изгибных колебаний пластинки от давления по формулам для несжимаемой и сжимаемой жидкостей для двуокиси углерода. Из рис. 2, b видно, что частоты по модели несжимаемой жидкости выше частот по модели для сжимаемой жидкости из-за увеличения плотности, причем с ростом давления разность частот колебаний возрастает.

Рис. 2.

Зависимость первой частоты изгибных колебаний пластинки  f1 (MHz) от давления p1 (MPa): (а) для разных газов: ρ1 = 0.1785 (гелий), 1.2928 (воздух), 1.9768 (двуокись углерода) kg/m3 (пунктирная, штриховая, сплошная линии соответственно); (b) по формулам для несжимаемой (2.14) и сжимаемой (3.7) жидкостей для двуокиси углерода ρ1 = 1.9768 kg/m3 (пунктирная, штриховая линии соответственно).

5. Заключение. Хорошо известно из литературы (например, [1–3]), что собственные частоты изгибных колебаний пластины при ее контакте с жидкостью значительно снижаются. Это объясняется влиянием присоединенной массы жидкости. Установлено [15, 16], что учет разности площадей противоположных поверхностей пластины, образующейся при ее изгибе, может оказывать повышающее влияние на собственные частоты. Учет этого эффекта приводит к появлению распределенной поперечной силы, равной произведению кривизны срединной поверхности и среднего давления на поверхности пластины.

Одновременное влияние указанных факторов на низшую частоту колебаний в случае несжимаемой жидкости зависит от отношения среднего давления к модулю упругости материала, плотностей материала и жидкости и отношения длины пластины к ее толщине. Для реальных параметров характерно превалирующее влияние плотности среды над давлением в ней. Однако давление может оказывать заметное влияние на результат.

Для сжимаемой жидкости влияние носит более сложный характер, так как присоединенная масса зависит от скорости звука и от самой частоты колебаний. Кроме того, давление и плотность газовой среды не являются независимыми.

Влияние контактирующей среды на низшую частоту колебаний является значительным для весьма тонких пластин и пленок с низким модулем упругости. Учет его необходим особенно в случае элементов микро- и наноразмерных толщин.

С ростом давления собственная частота колебаний возрастает. В случае легких газов (водород, гелий) влияние давления может превалировать над их плотностью. Эти результаты могут быть использованы при моделировании колебаний пластинок, контактирующих с жидкостью и газом, в том числе микро- и наноразмеров.

Работа проведена в порядке выполнения государственного задания (№ 0246-2019-0088).

Таблица 1.

Первая собственная частота изгибных колебаний пластинки, p1, MPa, f1, MHz

p1 0.1 0.1 2 2
α 0.0138 0.0138 0.2761 0.2761
μ 0 0.0078 0 0.1568
a –0.0138 –0.0059 –0.2754 –0.1027
Z (3.7) 1.0138 1.0059 1.2761 1.1027
f1 (3.7) 6.6108 6.5850 7.4170 6.8945
f1 (a3 = 0) (3.9) 6.6108 6.5850 7.4150 6.8946
f1 (a2 = 0) 6.5663 6.5661 6.8106 6.7363
f1 (3.10) 6.6108 6.5850 7.4171 6.8945

Список литературы

  1. Гонткевич В.С. Собственные колебания оболочек в жидкости. Киев: Наукова думка, 1964. 102 с.

  2. Ильгамов М.А. Колебания упругих оболочек, содержащих жидкость и газ. М.: Наука, 1969. 180 с.

  3. Попов A.JI., Чернышев Г.Н. Механика звукоизлучения пластин и оболочек. М.: Физматлит. 1994. 208 с.

  4. Нестеров С.В. Изгибные колебания квадратной пластины, защемленной по контуру // Изв. РАН. Механика твердого тела. 2011. № 6. С. 159–165.

  5. Денисов С.Л., Копьев В.Ф., Медведский А.Л., Остриков Н.Н. Исследования проблем долговечности ортотропных полигональных пластин при широкополосном акустическом воздействии с учетом эффектов излучения // Изв. РАН. Механика твердого тела. 2020. № 5. С. 138–150. https://doi.org/10.31857/S0572329920030058

  6. O’Connell A.D., Hofheinz M., Ansmann M. et al. Quantum ground state and single-phonon control of a mechanical resonator // Nature. 2010. V. 464. P. 697–703. https://doi.org/10.1038/nature08967

  7. Burg T.P., Godin M., Knudsen S.M. et al. Weighing of biomolecules, single cells and single nanoparticles in fluid // Nature. 2007. V. 446. P. 1066–1069. https://doi.org/10.1038/nature05741

  8. Husale S., Persson H.H.J., Sahin O. DNA nanomechanics allows direct digital detection of complementary DNA and microRNA targets // Nature. 2009. V. 462. P. 1075–1078. https://doi.org/10.1038/nature08626

  9. Raman A., Melcher J., Tung R. Cantilever dynamics in atomic force microscopy // Nano Today. 2008. V. 3. № 1–2. P. 20–27. https://doi.org/10.1016/S1748-0132(08)70012-4

  10. Eom K., Park H. S., Yoon D. S., Kwon T. Nanomechanical resonators and their applications in biological/chemical detection: Nanomechanics principles // Physics Reports. 2011. V. 503. № 4–5. P. 115–163. https://doi.org/10.1016/j.physrep.2011.03.002

  11. Stassi S., Marini M., Allione M. et al. Nanomechanical DNA resonators for sensing and structural analysis of DNA-ligand complexes // Nature Communications. 2019. V. 10. P. 1690. https://doi.org/10.1038/s41467-019-09612-0

  12. Jaber N., Hafiz M.A.A., Kazmi S.N.R. et al. Efficient excitation of micro/nano resonators and their higher order modes // Scientific Reports. 2019. V. 9. P. 319. https://doi.org/10.1038/s41598-018-36482-1

  13. SoltanRezaee M., Bodaghi M. Simulation of an electrically actuated cantilever as a novel biosensor // Scientific Reports. 2020. V. 10. P. 3385. https://doi.org/10.1038/s41598-020-60296-9

  14. Tavakolian F., Farrokhabadi A., SoltanRezaee M., Rahmanian S. Dynamic pull-in of thermal cantilever nanoswitches subjected to dispersion and axial forces using nonlocal elasticity theory // Microsystem Technologies. 2019. V. 25. № 3. P. 19–30. https://doi.org/10.1007/s00542-018-3926-y

  15. Ильгамов М.А. Влияние давления окружающей среды на изгиб тонкой пластины и пленки // ДАН. 2017. Т. 476. № 4. С. 402–405.

  16. Ильгамов М.А. Влияние поверхностных эффектов на изгиб и колебания нанопленок // ФТТ. 2019. Т. 61. № 10. С. 1825–1830.

  17. Ilgamov M.A., Khakimov A.G. Influence of pressure on the frequency spectrum of micro and nanoresonators on hinged supports // J. Appl. Comput. Mech. 2021. V. 7. № 2. P. 977–983. https://doi.org/10.22055/JACM.2021.36470.2848

  18. Timoshenko S.P., Young D.H., Weaver W.  Vibration Problems in Engineering. New York: John Wiley & Sons. 1974.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал