Известия РАН. Механика твердого тела, 2020, № 1, стр. 48-55

Введение. Классические подходы, используемые для описания фазово-структурных превращений, обычно предполагают введение дополнительных параметров в функционал свободной энергии и определяющие уравнения. В этом случае новые параметры определяются с помощью дополнительных термодинамических соотношений. Подробное описание методов и подходов к анализу возможного существования новых фаз материала приведено в работах [1, 2]. Особого внимания заслуживает цикл работ С.А. Кукушкина и А.В. Осипова, посвященный изучению физики образования и эволюции зародышей новой фазы в материале и влияния их на структурные изменения (смотри, например, [3, 4]). Обширный теоретический и экспериментальный материал, посвященный указанной выше проблеме, тем не менее, не позволяет детально описать динамические процессы, протекающие в материале, предшествующие его фазово-структурному превращению [5–7].

В работе на примере одноосного нагружения стержня конечной длины, поведение материала которого описывается исходя из модели двухкомпонентного континуума [8] показывается существенная роль динамических процессов на перестройку материала, а также выводится уравнение, определяющее деформацию образца, решение которого качественно описывает динамический характер структурных превращений.

Предлагаемая двухкомпонентная модель позволяет учесть роль динамики при переходе материала из одного состояния в другое, с помощью источниковых членов в уравнениях баланса массы. При этом показана роль характерных времен релаксации (времени “жизни” новых частиц фазы) на диссипацию механической энергии при переходе материала из одного состояния в другое. Определено уравнение состояния, связывающее шаровую часть тензора напряжений с шаровой частью тензора деформаций, которое зависит от концентрации частиц новой фазы и “регулируется” источниковыми членами, определяющими обмен частиц между компонентами. Полученные характерные кривые поведения уравнения состояния для сугубо нестационарного одноосного нагружения стержня указывают на наличие высокочастотных колебаний при переходе из одного состояния материала в другое, при этом спектр частот по своим значениям близок экспериментальным значениям [5].

1. Уравнение состояния. Рассмотрим одномерный образец, кристаллическая решетка которого содержит примеси и дефекты и будем моделировать ее следующей реологической моделью. Предположим, что кристаллическая решетка представляет собой одномерную цепочку, состоящую из одинаковых масс, которые соединены с соседними одинаковыми нелинейными пружинами. Известно, что, когда примесь растворена в материале, некоторые частицы примеси встраиваются в атомарные связи решетки, нарушают их и создают новые связи, жесткость которых значительно меньше, чем жесткости исходных связей. Таким свойством обладают, например, атомы растворенного в металле водорода [9]. Аналогичный эффект возникает в местах скопления дефектов решетки: вакансий, дислокаций и пр. Будем считать, что масса атома примеси много меньше массы атома решетки. В этом случае связь (пружинку) в которую встроился атом примеси, можно заменить менее жесткой пружиной, не учитывая массу атома примеси из-за ее малости. Соединяя элементы со старыми и новыми связями последовательно, мы получаем модель решетки с осажденными частицами примеси. Будем рассматривать кристаллическую решетку материала в рамках двухкомпонентной модели и предполагать, что она состоит из атомов двух компонент (типов, фаз). Роль первой компоненты (основная структура) играет кристаллическая решетка материала с атомами, соединенными неискаженными связями; вторая компонента – атомы, соединенные ослабленными связями (“дефектная” структура). При воздействии динамических нагрузок, например, в результате нагружения образца, межатомные связи могут искажаться (разрываться) и частицы первой компоненты (фазы) могут переходить во вторую и наоборот. С помощью предложенной реологической модели в [8] была получена зависимость модуля упругости от концентрации частиц новой фазы (частиц, соединенных ослабленными связями). Связь между относительной деформацией ${\varepsilon }$ и напряжением ${\sigma }$ в такой решетке может быть записана следующим образом

Здесь $E$ – эквивалентный модуль Юнга, определяющийся модулем Юнга, ${{E}_{0}}$, чистого материала (без примеси и дефектов), модулем Юнга, ${{E}_{Н}}$, все связи которого ослаблены (заняты частицами примеси), а так же числом атомов материала ${{N}_{0}}$ в единице объема, соединенных неискаженными связями, и числом атомов N⁺ в единице объема, соединенных связями меньшей жесткости (${{n}_{0}}{\text{\;}}$, n⁺ – соответствующие безразмерные концентрации частиц первой и второй фазы).

В общем случае концентрации ${{n}_{0}}{\text{\;}}$, n⁺ зависят от деформации материала, уравнение (1.1) является сложным нелинейным уравнением состояния среды и может быть записано в виде

При ${{n}^{ + }}~ \to {\text{\;}}0$ можно считать, что в материале отсутствуют ослабленные связи и дефекты и уравнение (1.2) сводится к известному закону Гука. При ${{n}^{ + }}~ \to {\text{\;}}{{n}_{\infty }}$, где $~{{n}_{\infty }}$ – некоторое предельное значение концентрации дефектов, очевидно, появление новой структуры с другим модулем упругости.

Заметим, что полученное уравнение состояния (1.2) хорошо согласуется со статистической моделью образования гидридной фазы в наводороженных металлах, предложенной в работах [10, 11].

2. Постановка задачи. Рассмотрим одноосное нагружение стержня конечной длины, поведение материала которого описывается исходя из модели двухкомпонентной сплошной среды. Вывод системы уравнений двухкомпонентного континуума приведен, например, в [8], поэтому запишем здесь только окончательные соотношения для одномерного случая. Уравнения баланса импульса стержня имеют вид:

Здесь ${\rho }$ – плотность стержня, $u\left( {x,t} \right)$ – продольное перемещение точек стержня и ${\varepsilon } = \partial u{\text{/}}\partial x$. Предполагается, в начальный момент времени $t = 0$ стержень находился в покое

Один конец стержня жестко заделан

а ко второму свободному концу в момент времени прикладывается зависящая от времени нагрузка ${{{\sigma }}_{0}}\left( t \right)$: где l – длина стержня. Уравнение состояния материала стержня, учитывающее структурные превращения материала (1.2) перепишем в виде где ${\kappa } = {\text{\;}}{{E}_{{\text{H}}}}{\text{/}}{{E}_{0}}$. Уравнение баланса числа частиц в элементарном объеме для первой и второй компоненты имеют вид

Здесь α, β – положительные коэффициенты. Предполагаем, что при t = 0 концентрации частиц первой и второй компоненты заданы следующим образом

В этом случае, в начальный момент времени основная структура (первая компонента) не содержит дефектов и их образование существенно зависит от свойств материала и параметров нагружения. При получении системы определяющих уравнений (2.1)−(2.8) из общих уравнений двухкомпонентной модели сплошной среды, был сделан ряд упрощений, которые поясним ниже. Уравнение (4) определяет динамическое поведение основной структуры материала стержня. Уравнение динамики “дефектной структуры”, которая может ослаблять основную, при пренебрежении силами инерции приводит к определению скорости частиц этой среды по формуле, аналогичной формуле Дарси, но с коэффициентом диффузии, зависящим от деформации.

Уравнения баланса масс (2.6), (2.7), записанные через концентрации, не содержат конвективной диффузионной части. Таким образом, здесь мы рассматриваем предельный случай, когда можно пренебречь скоростью диффузии дефектов и можно считать, что структурные изменения по всей длине образца происходят “почти” мгновенно. Как известно из экспериментальных данных, скорость таких изменений действительно может быть много больше скорости звука в материале [6].

Заметим, что источниковые члены в правой части балансовых уравнений (2.6)–(2.7) в общем случае зависят от деформаций образца. Каждый из коэффициентов α, β характеризует скорость обмена между частицами основной структуры (первой компоненты) и второй фазы, атомы которой соединены ослабленными связями.

3. Метод решения. Нелинейная система определяющих уравнений (2.1)−(2.8), описывающая динамику одномерного образца, имеющего внутреннюю структуру, поддается только численному анализу. Ограничимся здесь приближенным решением и получением результатов, качественно описывающих структурную перестройку материала.

Используя начальные условия (2.8) и предполагая, что ${\alpha }\left( {\varepsilon } \right) = {\text{\;}}{{{\alpha }}_{0}} = {\text{const}}$, исключим из системы (2.6)–(2.7) концентрацию $~{{n}_{0}}\left( t \right)$. Тогда для концентрации частиц второй компоненты (фазы) получим следующее уравнение

Здесь и далее опускаем “+” в обозначении концентрации частиц второй компоненты. Выразим $n\left( t \right){\text{\;}}$ из уравнения состояния (2.5) через σ и ε

и подставим (3.2) в уравнение (3.1). В результате получим следующее уравнение, связывающее напряжение и деформацию

Вернемся теперь к уравнению колебаний стержня (2.1) и используя метод Бубнова–Галеркина, построим его решение. Будем искать перемещение $u\left( {x,t} \right)$ в виде

Заметим, что используя это приближение, мы пренебрегаем волновыми процессами в стержне. При рассматриваемом нагружении основной интерес представляет асимптотическое поведение, поэтому будем предполагать такое распределение перемещений $u\left( {x,t} \right)$ по длине стержня. Подставляя (3.4) в уравнение (4) и применяя процедуру Бубнова–Галеркина, получим

где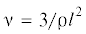 . Подставляя (3.5) в (3.3), получим следующее уравнение для определения деформации стержня где ${\lambda } = {\nu \kappa }{{E}_{0}}{\text{/}}({\kappa }({{{\alpha }}_{0}} + {\beta }) + {{{\alpha }}_{0}}{\psi })$, $~{\mu } = {{{\alpha }}_{0}} + {\beta }$, $f({\varepsilon },{{{\sigma }}_{0}}) = \left( {{\nu }{{{{\dot {\sigma }}}}_{0}} - {\dddot \varepsilon }} \right){\text{/}}\left( {{\nu }~{{{\sigma }}_{0}} - {\ddot {\varepsilon }}} \right)$.

Уравнение (3.6), определяющее деформацию стержня содержит диссипативное слагаемое ${\lambda }\left( {\varepsilon } \right){\dot {\varepsilon }}$, определяющее вязкость материала. Коэффициент ${\lambda }\left( {\varepsilon } \right)$ существенно зависит как от начальной концентрации атомов основной структуры, так и от параметров, определяющих скорость перехода частиц одной фазы в другую. Решение сугубо нелинейного уравнения (3.6) зависит от поведения коэффициента ${\lambda }\left( {\varepsilon } \right)$. Предположим, что $f\left( {{\varepsilon },{{{\sigma }}_{0}}} \right) \ll {\mu }$, тогда уравнение (3.6) можно может быть записано следующим образом

В начальный момент времени стержень находился в покое и

Положим ${\alpha (}\varepsilon {\text{)}} = {{{\alpha }}_{0}}~ = {\text{const}}$, а ${\beta }\left( {\varepsilon } \right) = {{{\beta }}_{0}}{{e}^{{ - {\gamma \varepsilon }}}}$ (где $\gamma $ – некоторый коэффициент). Тогда, решая уравнение (3.1), в предельном случае получим для частиц новой фазы следующее выражение

где ${\delta } = {{{\beta }}_{0}}{\text{/}}{{{\alpha }}_{0}}$. Подставка (3.8) в (2.5) дает уравнение состояния, зависящее не только от параметров материала, но и от коэффициентов α, ${\beta }$, характеризующих скорость обмена между частицами основной структуры и второй компоненты.

На рис. 1 приведена зависимость напряжения ${\sigma } = \bar {\sigma } \times {{10}^{9}}$ от деформации, вычисленная по формулам (2.5) и (3.8) для следующих значений параметров ${{E}_{0}} = 1.5 \times {{10}^{{11}}}$ Па, ${\kappa } = 0.1$, $~{\psi } = 1$, ${\delta } = 50$, ${\gamma } = 80$, что примерно соответствует таким материалам как сталь. Данная петлеобразная зависимость ${\sigma }\left( {\varepsilon } \right)$ определяет типичный фазовый переход первого рода. Эта диаграмма имеет три характерных участка изменения: 1 − возрастающий, 2 − ниспадающий, 3 − опять возрастающий с модулем отличным от модуля первого участка. Таким образом, если к стержню, содержащему примесь, приложить растягивающую нагрузку, которая увеличивается со временем, то процесс деформации стержня можно условно разбить на три этапа. На первом этапе, до достижения некоторой критической нагрузки, стержень растягивается по закону Гука. При достижении растягивающей силы своего критического значения в материале стержня начинается второй этап − происходит фазовый переход первого рода. В материале стержня начинают образовываться области с менее жесткими связями. Эти области увеличиваются и затем образуют однородную новую фазу. При дальнейшем увеличении растягивающего усилия происходит структурная перестройка материала, сопровождающаяся резким увеличением его деформации, и переход на третий участок диаграммы ${\sigma }\left( {\varepsilon } \right)$, минуя область неустойчивости (участок 2). После завершения фазового перехода материал стержня снова будет вести себя по закону Гука, но с меньшим модулем упругости (участок 3).Таким образом, при достижении критического значения прикладываемого напряжения, которое для данных параметров материала примерно равна $1.6 \times {{10}^{9}}$ Па возможна структурная перестройка материала (переход с первого участка графика на второй) и резкое уменьшение модуля упругости.

С помощью уравнения (3.7) получим зависимость деформации от времени. Предполагаем, что прикладываемая к свободному концу стержня нагрузка меняется по следующему закону ${{{\sigma }}_{0}}\left( t \right) = {{{\sigma }}_{0}}t~H\left( t \right)$, где ${{{\sigma }}_{0}}$ – амплитуда прикладываемого напряжения, H(t) – функция Хевисайда. На рис. 2 приведены результаты численного решения уравнения для приведенных выше параметров материала (${\rho } = 6 \times {{10}^{3}}$ кг/м³), а именно построена зависимость деформации от времени $t = {\tau } \times {{10}^{2}}.$ В момент времени, когда значения прикладываемого напряжения достигает критического значения ${{{\sigma }}_{0}}(t) \approx 1.6$ × 10⁹ Па в соответствии с диаграммой ${\sigma } - \varepsilon $ происходит переход материала в другое структурное состояние (рис. 1). Действительно, при этом происходит резкое увеличение значения деформации и наблюдаются ее высокочастотные осцилляции, вызванные диссипацией энергии (смотри рис. 3). При дальнейшем нагружении материала (участок 3 на рис. 2) скорость роста деформации увеличивается, что соответствует, как уже отмечалось выше, резкому уменьшению модуля упругости материала в результате структурной перестройки.

Заметим, что в работе [7] на примере водородного охрупчивания построена термодинамическая и кинетическая теория такого фазового перехода. Показано, что фазовый переход происходит при растягивающих нагрузках меньших, чем значение максимума кривой ${\sigma }\left( {\varepsilon } \right)$.

Таким образом, предложенная в данной работе модель, построенная с помощью классической механики многокомпонентного континуума предлагает качественное описание структурной перестройки материала и позволяет описать высокочастотные осцилляции, сопровождающие фазовый переход. Здесь мы пренебрегали конвективной диффузионной частью в уравнениях баланса масс и определяемые деформации не меняются по длине стержня (не зависят от пространственной координаты). При нагружении реальных образцов зоны ослабления связей появляются в различных точках стержня и необходимо учитывать их диффузию при увеличении динамических нагрузок.

Заключение. Рассмотрено нагружение металлического стержня, материал которого содержит примеси и описывается моделью двухкомпонентного континуума. Предлагаемая двухкомпонентная модель позволяет учесть роль динамики при переходе материала из одного состояния в другое, с помощью источниковых членов в уравнениях баланса массы. Полученное решение демонстрирует существенное влияние эволюционных процессов на перестройку структуры, определенной уравнением состояния, зависящим от концентрации “дефектной” структуры. Данное приближенное решение исходной задачи качественно описывает динамические эффекты при переходе от одного устойчивого положения структуры к другому.

Показано, что структурно-фазовые превращения в материале при динамическом нагружении всегда сопровождаются характерными колебаниями, частота которых зависит от источниковых членов, то есть от скорости обмена частиц одной фазы с другой. После завершения фазового перехода материал образца характеризуется эффективным модулем упругости, по величине меньшим, чем исходный. Дальнейшие исследования предполагают учитывать влияние температуры на перестройку материала, что особенно актуально при лазерном воздействии на материал образца.

Работа выполнена при поддержке Программы фундаментальных исследований президиума Российской академии наук на 2019 г. № 31 “Фундаментальные исследования физико-технических проблем энергетики”.