Химия твердого топлива, 2021, № 3, стр. 43-47
ОПРЕДЕЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ ФРАКЦИИ ПЕРВИЧНОЙ КАМЕННОУГОЛЬНОЙ СМОЛЫ АДДИТИВНЫМ МЕТОДОМ
Д. Е. Айтбекова 1, *, М. И. Байкенов 1, **, Н. Ж. Балпанова 1, ***, А. Тусипхан 1, ****, Г. Г. Байкенова 2, 3, Т. А. Яркова 4, *****, А. М. Гюльмалиев 5, ******
1 Карагандинский университет имени академика Е.А. Букетова
100028 Караганда, Республика Казахстан
2 Карагандинский экономический университет Казпотребсоюза
100009 Караганда, Республика Казахстан
3 Южно-Уральский государственный университет
454080 Челябинск, Россия
4 ФГБОУ ВО Российский экономический университет имени Г.В. Плеханова
117997 Москва, Россия
5 ФГБУН Институт нефтехимического синтеза имени А.В. Топчиева РАН
119991 Москва, Россия
* E-mail: darzhan91@mail.ru
** E-mail: murzabek_b@mail.ru
*** E-mail: nazerke_90@mail.ru
**** E-mail: almas_kz_22@mail.ru
***** E-mail: tat772003@list.ru
****** E-mail: gyulmaliev@ips.ac.ru
Поступила в редакцию 15.08.2020
После доработки 15.08.2020
Принята к публикации 09.12.2020
Аннотация
Приведены результаты расчета термодинамических функций фракции первичной каменноугольной смолы с температурой выкипания до 300°С для моделирования продуктов гидрогенизации с помощью аддитивного метода. На модельных реакциях гидрирования о-крезола показано, что в области температур 700 K реакция гидрирования ароматического кольца более вероятна, чем гидрогенолиз связи метильных и гидроксильных групп с ароматическим кольцом. Для суммарного состава каменноугольной смолы с температурой выкипания до 300°С, с учетом аддитивности термодинамических функций, в интервале температур 298–1000 K вычислены теплоемкость, энтальпия, энтропия и энергия Гиббса. Показано, что полученные данные могут быть использованы при моделировании процесса гидрогенизационной переработки фракции первичной каменноугольной смолы.
Одной из главных проблем коксохимической промышленности является образование в большом количестве первичной смолы из каменных углей (2–18%), которую не удается утилизировать в полном объеме [1]. Один из способов переработки образующейся смолы – гидрогенизационные процессы, продукты которых являются сырьем для дальнейших химических превращений в востребованные на рынке соединения.
Для термодинамических исследований углехимических процессов, в частности гидрогенизационной переработки угля, первичной каменноугольной смолы (ПКС) и ее фракций в широком температурном диапазоне, необходимо иметь данные по значению термодинамических функций, таких как теплоемкость, энтальпия, энтропия, свободная энергия Гиббса. Один из теоретических методов расчета этих функций предложен в работе [2].
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
В качестве объекта исследования была использована фракция с концом кипения 300°С, которую отбирали из каменноугольной смолы дистилляционной разгонкой. Каменноугольная смола была получена в процессе коксования угля на предприятии АО “ШубаркольКомир” (Республика Казахстан, г. Караганда).
Хромато-масс-спектрометрический анализ фракций проводили на газовом хроматографе фирмы AgilentTechnologies 7890A с масс-спектрометрическим детектором 5975С. Для анализа использовалась подвижная фаза SE марки А, хроматографическая колонка НР-5НS, длина которой 30 м, диаметр 0.25 мм, толщина адсорбента внутри капилляра 0.25 мкм. Температура колонки изменялась равномерно от 60 до 300°C с течением времени; гелий подавался со скоростью 8 мл/с.
Образец вводили в колонку автосемплером 7683В объемом 1 мкл. После разделения в колонке исследуемый образец поступал в ионизационную камеру масс-спектрометра. В камере, по мере поступления, молекулы разбиваются на осколки электронным ударом энергией 70 эВ, при температуре 250°C. Осколки, вытянутые из ионизационной камеры электростатическим полем, поступали в квадрупольный конденсатор, с помощью которого получали масс-спектры компонентов исследуемого образца.
Хроматограммы и масс-спектры обрабатывали с помощью программы MSDChemStationE02.00.493. Для идентификации веществ по масс-спектрам использовали базу данных масс-спектров NIST-8.
Расчет термодинамических функций проводили аддитивным методом, разработанным в [2–4]. Расчет проводили по набору параметров, учитывающих гибридные состояния углеродных атомов и числа атомов водорода, связанных с ними химической связью. Метод позволяет рассчитать температурную зависимость термодинамических функций в интервале от 298 до 1000 K для углеводородов произвольной структуры. Термодинамические функции молекул представляются в следующем виде:
где ${{f}_{\mu }}$ − величина свойства Φ, приходящаяся на μ-й тип структурной группы.Расчет температурной зависимости Cp фрагментов проводился по квадратичной функции:
где a, b, c – эмпирические коэффициенты.Изменения энтальпии ∆HM и энтропии ∆SM молекулы M в зависимости от температуры вычислялись по следующим формулам:
(3)
$\Delta {{S}_{M}}(T) = \Delta {{S}_{{298}}} + \mathop \smallint \limits_{298}^T \Delta {{C}_{{{{p}_{M}}}}}(T)d(\ln T).$С учетом (2) из формул (3) имеем
(4)
$\begin{gathered} \Delta S(T) = \Delta {{S}_{{298}}} + \alpha \ln \frac{T}{{298}} + \\ \, + \beta (T - 298) + \frac{\gamma }{2}[{{T}^{2}} - {{298}^{2}}], \\ \end{gathered} $Свободная энергия Гиббса ΔG вычислялась по формуле
Для расчета термодинамических функций фракции первичной каменноугольной смолы с концом кипения 300°С использовались количественные данные элементного состава и функциональных групп фракции ПКС.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
На первом этапе исследования на примере молекулы фенола проведено сравнение результатов расчета аддитивным методом термодинамических функций с литературными данными. В табл. 1 приведены полученные результаты аддитивного метода расчета теплоемкости, энтропии, энтальпии и свободной энергии Гиббса в сравнении с литературными данными [5].
Таблица 1.
Сравнение результатов аддитивного метода расчета термодинамических функций молекулы фенола (в газовом состоянии) с литературными данными
| T, K | Cp, кДж/(моль · K) | ΔH, кДж/моль | S, Дж/(моль · K) | ΔG, кДж/моль | ||||
|---|---|---|---|---|---|---|---|---|
| [5] | метод * | [5] | метод * | [5] | метод * | [5] | метод * | |
| 298 | 103.62 | 90.73 | –96.42 | –82.69 | 315.81 | 338.46 | –32.91 | –25.5 |
| 300 | 104.25 | 91.27 | –96.51 | –82.81 | 316.48 | 339.05 | –32.53 | –25.16 |
| 400 | 135.86 | 117.5 | –100.9 | –88.8 | 350.94 | 369.02 | –10.51 | –6.16 |
| 500 | 161.78 | 140.3 | –104.3 | –94.08 | 384.14 | 397.75 | 12.51 | 15.24 |
| 600 | 182.29 | 159.6 | –106.9 | –98.85 | 415.5 | 425.09 | 36.09 | 38.23 |
| 700 | 198.62 | 175.5 | –108.9 | –103.2 | 444.89 | 450.92 | 60.12 | 62.17 |
| 800 | 211.94 | 187.9 | –110 | –107.1 | 472.27 | 475.2 | 84.32 | 86.42 |
| 900 | 222.99 | 196.8 | –111.5 | –110.7 | 497.89 | 497.89 | 108.8 | 110.32 |
| 1000 | 232.33 | 202.2 | –112.2 | –114.2 | 521.88 | 518.95 | 133.3 | 133.22 |
Представленные в табл. 1 данные показывают, что аддитивный метод удовлетворительно воспроизводит температурную зависимость термодинамических функций в широком интервале температур.
Поскольку именно крезолы составляют значительную часть (26%) фракции первичной каменноугольной смолы с концом выкипания до 300°С, то в качестве модельного углеводорода был выбран о-крезол:
В табл. 2 приведены значения свободной энергии Гиббса $\Delta G~$ компонентов реакций І–ІІІ (основные реакции гидрогенизации первичной каменноугольной смолы: І – деалкилирование, ІІ – дегидроксилирование, ІІІ – гидрирование).
Таблица 2.
Энергия Гиббса для компонентов реакций І–ІІІ при различных температурах для состояния идеального газа, ΔG (кДж/моль)
| Т, K | о-Крезол [5] | Фенол [5] | Метан [5] | Толуол [5] | Вода [5] | 2-Метил-циклогексанол* |
|---|---|---|---|---|---|---|
| 298 | –37.10 | –32.90 | –50.87 | 122.09 | –228.77 | –83.10 |
| 300 | –36.51 | –32.50 | –50.70 | 122.55 | –228.68 | –81.68 |
| 400 | –4.86 | –10.50 | –42.16 | 147.79 | –224.08 | –7.82 |
| 500 | 28.01 | 12.52 | –32.87 | 174.59 | –219.22 | 70.45 |
| 600 | 61.63 | 36.09 | –23.07 | 202.31 | –214.20 | 151.63 |
| 700 | 95.84 | 60.12 | –12.81 | 230.73 | –209.01 | 234.24 |
| 800 | 130.34 | 84.32 | –2.35 | 259.50 | –203.69 | 316.79 |
| 900 | 165.09 | 108.80 | 8.33 | 288.60 | –198.29 | 397.77 |
| 1000 | 199.92 | 133.30 | 19.18 | 317.82 | –192.76 | 475.67 |
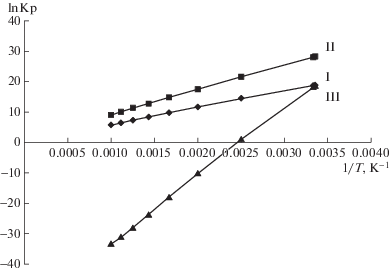
На рис. 1 представлены зависимости логарифма константы равновесия реакций I–III от температуры. Анализ графика показывает, что в области температур T = 700 K реакция гидрирования термодинамически более вероятна, чем реакции деалкилирования и дегидроксилирования.
Аддитивный метод также может быть применен и для расчета термодинамических функций тяжелого сырья сложного состава [4]. Для органических соединений, состоящих из атомов элементов C, H, N, O, S с брутто-формулой CxHyNmOnSz, где x = C(%)/12, y = H(%), m = N(%)/14, n = O(%)/16, z = S(%)/32, молекулярная масса М, вычисленная по округленным атомным массам, равна [6]:
(6)
$12{{n}_{{\text{C}}}} + {{n}_{{\text{H}}}} + 14{{n}_{{\text{N}}}} + 16{{n}_{{\text{O}}}} + 32{{n}_{{\text{S}}}} = M,$Данные хромато-масс-спектрометрического анализа фракции первичной каменноугольной смолы до 300°С приведены в табл. 3.
Таблица 3.
Индивидуальный химический состав фракции ПКС до 300°С
| Соединение | Количес- тво, % | Соединение | Количе-ство, % |
|---|---|---|---|
| Фенол | 10.87 | 1-Гексадецен | 0.48 |
| Этоксибензол | 0.54 | Гексадекан | 1.75 |
| 1,2-Диэтилбензол | 0.35 | 1,6-Диметил-4-(1-метилэтил)-нафталин | 1.4 |
| Индан | 0.30 | Гептадекан | 1.73 |
| 2-Метилфенол | 8.41 | Октадекан | 1.48 |
| 3-Этилфенол | 4.64 | Нонадекан | 1.16 |
| 4-Метилфенол | 17.69 | Эйкозан | 1.46 |
| Ундекан | 0.28 | 2,3-Диметил-2-циклопентен-1-он | 0.18 |
| 2,6-Диметилфенол | 0.88 | 2,3-Дигидро-1,2-диметил-1H-инден | 0.17 |
| 2-Этилфенол | 6.21 | 3-Метил-1,2-бензолдиол | 0.26 |
| 2,4-Диметилфенол | 6.36 | 2,3-Дигидро-5,6-диметил-1H-инден | 0.31 |
| 2,3-Диметилфенол | 0.70 | 4-Метил-1,2-бензолдиол | 0.16 |
| 3,4-Диметилфенол | 0.25 | 3-Метил-4-изопропилфенол | 0.16 |
| Нафталин | 0.62 | 4-Метокси-1,3-бензолдиамин | 0.62 |
| Додекан | 0.52 | 2,3-Дигидро-1H-инден-5-ол | 0.33 |
| 5,6-Диметил-1H-бензимидазол | 0.26 | 4-(2-Бутенил)-1,2-диметилбензол | 0.54 |
| 2-Этил-1H-бензимидазол | 0.75 | 6-Метил-4-инданол | 0.64 |
| 2-Этил-5-метилфенол | 1.72 | 1,2,3,4-Тетраметил-4-(1-метилэтенил)-бензол | 0.33 |
| 2-Этил-4-метилфенол | 0.97 | 2-Изопропил-3,6-диметилпиразин | 0.14 |
| 1-Этил-4-метоксибензол | 0.85 | 3,4-Дигидро-2,2-диметил-2H-1-бензопиран | 0.16 |
| 3-Этил-5-метилфенол | 2.84 | 1,7-Диметилнафталин | 0.16 |
| 2,4,6-Триметилфенол | 1.33 | p-(1-Этилвинил)-анизол | 0.14 |
| 1-Тридецен | 0.41 | 2,3,6-Триметилнафталин | 0.55 |
| Тридекан | 1.74 | 1-Нафталенол | 0.37 |
| 1-Метилнафталин | 0.50 | 2-Нафтилкарбамат | 0.16 |
| 1-(2-Бутенил)-2,3-диметилбензол | 0.37 | 2,3-Дигидро-3,3,5,7-тетраметил-1H-инден-1-он | 0.22 |
| 2-Метилнафталин | 1.99 | 1,4,6-Триметилнафталин | 0.16 |
| 2-Тетрадецен, (E)- | 0.37 | 1,6,7-Триметилнафталин | 0.49 |
| Тетрадекан | 1.62 | 2-Метил-1,1'-бифенил | 0.18 |
| 1-Этилнафталин | 0.21 | 2-Метил-1-нафталенол | 0.34 |
| 2,6-Диметилнафталин | 0.86 | 4-Метил-дибензофуран | 0.21 |
| 2,3-Диметилнафталин | 1.19 | E-14-Гексадеценаль | 0.19 |
| 1,3-Диметилнафталин | 0.26 | Z-5-Нонадецен | 0.21 |
| 1,6-Диметилнафталин | 0.78 | E-15-Гептадеценаль | 0.16 |
| 1-Пентадецен | 0.66 | Генэйкозан | 0.64 |
| Пентадекан | 1.82 | Тетракозан | 0.22 |
| 2,6,6-Триметил-1-(3-метил-1,3-бутадиенил)-1,3-циклогексадиен | 0.37 | 1-Метил-7-(1-метилэтил)-фенантрен | 0.26 |
| Неидентифицированные | 1.39 |
На основе полученных данных индивидуального химического состава были рассчитаны элементный и фрагментарный состав (табл. 4), молекулярная масса фракции ПКС до 300°С.
Таблица 4.
Результаты расчета количества атомов и структурных параметров на 1 моль фракции ПКС до 300°С
| Структурный параметр | Количество, моль | Структурный параметр | Количество, моль |
|---|---|---|---|
| С | 8.743 | –O– | 0.031 |
| H | 11.846 | –S– | – |
| N | 0.035 | –NH– | 0.034 |
| O | 0.791 | >C = | 2.029 |
| S | – | HC= | 3.757 |
| –OH | 0.760 | >C< | 0.007 |
| –NH2 | 0.001 | >CH- | 0.046 |
| –COOH | – | H2C< | 1.672 |
| –SH | – | H3C- | 1.240 |
По данным табл. 4 брутто-формула 1 моля фракции первичной каменноугольной смолы до 300°С может быть представлена в виде: C8.74H11.85N0.035O0.79 (M = 130 г/моль).
В рамках принятых структурных параметров невозможно однозначно различать изомеры и формы конденсации “среднестатистической структурной единицы”. Однако можно утверждать, что термодинамические функции всевозможных структур, удовлетворяющих данным табл. 4, будут иметь близкие значения, как в случае изомеров [4].
Термодинамические функции фракции ПКС до 300°С, вычисленные аддитивным методом, приведены в табл. 5.
Таблица 5.
Термодинамические функции фракции ПКС до 300°С
| T, K | Cp, кДж/(моль·K) | ΔH, кДж/моль | S, кДж/(моль·K) | ΔG, кДж/моль |
|---|---|---|---|---|
| 298 | 156.17 | –125.65 | 460.10 | 8.83 |
| 300 | 157.07 | –125.86 | 461.15 | 9.67 |
| 400 | 199.75 | –135.46 | 512.31 | 54.19 |
| 500 | 237.34 | –143.68 | 561.01 | 102.69 |
| 600 | 269.83 | –150.66 | 607.23 | 153.92 |
| 700 | 297.23 | –156.53 | 650.95 | 206.63 |
| 800 | 319.53 | –161.44 | 692.15 | 259.56 |
| 900 | 336.73 | –165.53 | 730.83 | 311.46 |
| 1000 | 348.84 | –168.96 | 766.98 | 361.09 |
ЗАКЛЮЧЕНИЕ
Проведенные исследования показывают, что аддитивные методы расчета термодинамических функций, не требующие экономических затрат на эксперимент, могут быть использованы для предварительной оценки тепловых характеристик, особенно при моделировании направленности и вероятности протекания типичных реакций переработки сложных органических систем.
Список литературы
Глущенко И.М. Теоретические основы технологии горючих ископаемых. М.: Металлургия, 1996. 296 с.
Gyulmaliev A.M., Popova V.P., Romantsova I.I., Krichko A.A. Calculation of thermodynamic function of coal liquids // Fuel. 1992. V. 71. № 11. P. 1329–1333. https://doi.org/10.1016/0016-2361(92)90062-S
Гюльмалиев А.М., Головин Г.С., Гладун Т.Г. Теоретические основы химии угля. М.: Московский государственный горный университет, 2003. 556 с.
Кадиев Х.М., Гюльмалиев А.М., Кубрин Н.А. // Нефтехимия. 2016. Т. 56. № 6. С. 584. [Petroleum Chemistry, 2016. V. 56. № 9. P. 805. https://doi.org/10.1134/S0965544116090073]https://doi.org/10.7868/S0028242116060071
Сталл Д., Вестрам Э., Зинке Г. Химическая термодинамика органических соединений. М.: Мир, 1971. 807 с.
Яркова Т.А., Гюльмалиев А.М. // ХТТ. 2018. № 2. С. 17. [Solid Fuel Chemistry, 2018. V. 52. № 2. P. 73. https://doi.org/10.3103/S036152191802012X]https://doi.org/10.7868/S0023117718020044
Дополнительные материалы отсутствуют.
Инструменты
Химия твердого топлива