Химия твердого топлива, 2021, № 2, стр. 54-59
АДСОРБЦИЯ САЛИЦИЛОВОЙ КИСЛОТЫ ИЗ ВОДНОЙ СРЕДЫ НА МИКРОПОРИСТОМ ГРАНУЛИРОВАННОМ АКТИВИРОВАННОМ УГЛЕ
А. К. Ракишев 1, *, М. Д. Веденяпина 1, **, С. А. Кулайшин 1, ***, Д. В. Курилов 1, ****
1 ФГБУН Институт органической химии имени Н.Д. Зелинского РАН
119991 Москва, Россия
* E-mail: askar@ioc.ac.ru
** E-mail: mvedenyapina@yandex.ru
*** E-mail: s.kulaishin@mail.ru
**** E-mail: kur-dv@mail.ru
Поступила в редакцию 06.08.2020
После доработки 08.12.2020
Принята к публикации 09.12.2020
Аннотация
Изучена кинетика адсорбции салициловой кислоты на микропористом гранулированном активированном угле (ГАУ) в водной среде. Показана высокая адсорбционная емкость ГАУ по этому веществу. Определены порядок адсорбции салициловой кислоты и энергия активации адсорбции.
ВВЕДЕНИЕ
Лекарственные препараты медицинского применения, например аспирин и салициловая кислота (СК), как и целый ряд других препаратов, являются биологически активными и подавляют рост и жизнедеятельность колоний микроорганизмов, используемых на очистных сооружениях для очистки стоков от вредных компонентов. Это приводит к тому, что стоки остаются не полностью очищенными, препараты попадают в окружающую среду и могут проникать в живые организмы. В работе [1] описано присутствие аспирина в форели, выловленной в оз. Боден (Boden-See). СК-метаболит аспирина – также широко используемый лекарственный препарат [2, 3].
Для предотвращения негативного влияния СК необходимо использовать методы либо ее извлечения, либо деградации в сточных водах до стадии биологической очистки. Адсорбция на активированных углях и других углеродных адсорбентах – эффективный метод удаления фармацевтических препаратов из водных растворов [4–14]. Эффективными адсорбентами для удаления фармацевтических препаратов, в том числе салициловой кислоты, являются микропористые активированные угли [14]. Ранее в работе [15] было показано, что углеродные материалы, применяемые для адсорбции фармацевтических препаратов (ФП) из водной среды, – эффективные адсорбенты. Сорбционная емкость по отношению к ФП обеспечивалась за счет высокой удельной поверхности и общего объема пор. Анализ ряда работ позволил заключить, что проблема очистки сточных вод может быть решена с использованием метода адсорбции. Важный вопрос в решении этой проблемы – это подбор с научной точки зрения подходящего адсорбента. В [11] был изучен активированный уголь Сибунит в процессе адсорбции СК.
В работе [16] был изучен микропористый адсорбент – гранулированный активированный уголь (ГАУ, GAC-2), показавший свою эффективность при очистке сточных вод от биологически активных органических соединений (БАОС) и ионов тяжелых металлов на очистных сооружениях. Образец имел нанесенные поверхностные группы железа. Известно, что поверхностные группы железа на активированных углях способствуют более высокому значению адсорбционной емкости по отношению к ионам тяжелых металлов [17]. В [18] показано, что ГАУ способен эффективно адсорбировать также и БАОС, например 2.4-дихлорфеноксиуксусную кислоту. Известно, что микропористые образцы активированных углей обладают значительной адсорбционной емкостью, как, например, активированный уголь из скорлупы кокосового ореха (АУКО) [19]. В настоящей работе изучена кинетика адсорбции СК на ГАУ.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
В работе использовали СК фирмы “Sigma-Aldrich Chemie”. Для исследований был взят углеродный адсорбент – гранулированный активированный уголь (ГАУ) фирмы “Wasserchemie” GmbH & Co. KG”, (производства Германии). Структурная формула СК приведена ниже:
Линейные размеры молекулы СК составляют 0.696 × 0.587 нм2; константа диссоциации кислоты pKa 2.97; растворимость в воде при 298 K – 8.21 г/л [13].
Для приготовления растворов использовали дистиллированную воду. Адсорбцию СК на ГАУ из водных растворов с заданной концентрацией проводили в термостатированной ячейке с обратным холодильником при постоянном перемешивании магнитной мешалкой (150 об/мин) при 25, 40 и 60°C. Концентрацию СК после адсорбции определяли методом УФ-спектроскопии по поглощению при 295 нм на приборе Hitachi U-1900. Кинетику адсорбции изучали по изменению концентрации СК во времени. Величину адсорбции qt (массу адсорбированной кислоты, приходящейся на 1 г адсорбента) рассчитывали по формуле
где mс – масса ГАУ, г; V – объем раствора, л; с0 и сt – концентрации СК, мг/л, в начале эксперимента и через время t, ч.Величину удельной поверхности и пористую структуру ГАУ определяли на объемной вакуумной статической установке ASAP2020M “Micromeritics” с использованием низкотемпературной адсорбции азота при 77 K. Текстурные характеристики образцов рассчитывали из изотерм адсорбции–десорбции с применением сервисной DFT-программы “Micromeritics” к прибору ASAP-2020М. Средний размер пор ГАУ, определенный методом Хорвата-Кавазое, составил 0.8 нм. Общая площадь поверхности по БЭТ равна 1513 м2/г.
Микроструктуру образцов изучали методом сканирующей электронной микроскопии с полевой эмиссией (FE-SEM) на электронном микроскопе Hitachi SU8000. Оптимизация аналитических измерений проведена в рамках описанного ранее подхода [20]. Перед съемкой образцы помещали на поверхность алюминиевого столика диаметром 25 мм, фиксировали при помощи проводящей липкой ленты. Морфология образцов исследовалась в нативных условиях для исключения поверхностных эффектов от напыления проводящего слоя [21]. Съемку изображений проводили в режиме регистрации вторичных электронов при ускоряющем напряжении 2–15 кВ и рабочем расстоянии 8–11 мм. Данные микроскопического исследования показали, что структура поверхности ГАУ образована частицами от 50 до 500 нм в виде глобул [18].
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
На рис. 1–3 приведены данные по кинетике адсорбции СК при температуре 25°C (рис. 1), 40°C (рис. 2) и 60°C (рис. 3) для различных исходных концентраций СК (50–200 мг/л) и массы ГАУ, равной 0.1 г. Кинетические кривые адсорбции СК на ГАУ обнаруживают вначале быстрый рост, а затем приближение к некоторому предельному значению адсорбции (qе), более высокому для больших начальных концентраций субстрата.
Рис. 1.
Кинетика адсорбции СК на ГАУ при 25°C и начальных концентрациях СК, мг/л: 1 – 200, 2 – 150, 3 – 125, 4 – 100, 5 – 75, 6 – 50; (а) в течение 2900 мин, (б) – 400 мин.
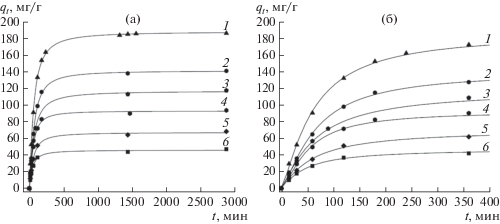
Рис. 2.
Кинетика адсорбции СК на ГАУ при 40°C и начальных концентрациях СК, мг/л: 1 – 200, 2 – 150, 3 – 125, 4 – 100, 5 – 75, 6 – 50.
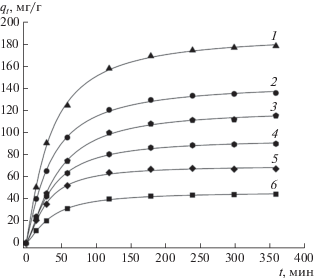
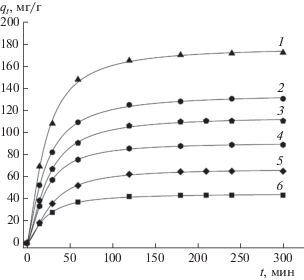
Рис. 3.
Кинетика адсорбции СК на ГАУ при 60°C и начальных концентрациях СК, мг/л: 1 – 200, 2 – 150, 3 – 125, 4 – 100, 5 – 75, 6 – 50.
Анализ кинетических кривых проводили в предположении протекания адсорбции по псевдопервому и псевдовторому порядкам. Уравнение псевдопервого порядка в дифференциальной форме (уравнение Лагергрена) имеет вид
где k1 – константа скорости адсорбции псевдопервого порядка (мин–1), qt – значение адсорбции, мг/г, в момент времени t, мин, и qe – равновесное значение адсорбции СК.После интегрирования при начальном условии qt = 0 выражение (1) принимает вид
В такой линейной форме уравнение псевдопервого порядка может быть применено для визуального анализа экспериментальных данных. Однако в интегральной нелинейной форме уравнение (2) псевдопервого порядка позволяет анализировать опытные данные, не прибегая ни к каким специальным преобразованиям:
В дальнейшем все вычисления приводили для нелинейных форм кинетических уравнений. Из уравнения (2) величины qe и k1 рассчитывали при помощи программы minerr, встроенной в систему Мathcad-15 [4, 5, 7, 9–11, 18, 19]. В табл. 1 приведены значения параметров уравнения (2), определенные при 25, 40 и 60°C для шести значений исходной концентрации СК. Высокие значения коэффициентов корреляции указывают на удовлетворительное соответствие уравнения псевдопервого порядка экспериментальным данным.
Таблица 1.
Кинетические параметры адсорбции СК на ГАУ
| T, °C | c0, мг/л | Псевдопервый порядок | Псевдовторой порядок | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| qe, мг/г | k1 ⋅ 10–2, 1/мин | $V_{0}^{1}$, мг/(г ⋅ мин) | R2 | $V_{0}^{{{\text{эксп}}}}$, мг/(г ⋅ мин) | qe, мг/г | k2 ⋅ 10–4 г/(мг ⋅ мин) | $V_{0}^{2}$, мг/(г ⋅ мин) | R2 | ||
| 25 | 200 | 184 | 1.1 | 2.02 | 0.998 | 1.96 | 193 | 0.83 | 3.09 | 0.992 |
| 150 | 139 | 1.0 | 1.39 | 1 | 1.27 | 147 | 0.95 | 2.06 | 0.989 | |
| 125 | 117 | 1.1 | 1.29 | 0.998 | 1.14 | 120 | 1.21 | 1.72 | 0.997 | |
| 100 | 92 | 1.3 | 1.20 | 0.999 | 0.98 | 96 | 1.92 | 1.78 | 0.983 | |
| 75 | 68 | 1.2 | 0.82 | 0.993 | 0.8 | 70 | 2.36 | 1.17 | 0.992 | |
| 50 | 46 | 1.5 | 0.69 | 0.994 | 0.68 | 47 | 4.51 | 1.02 | 0.993 | |
| 40 | 200 | 174 | 2.2 | 3.84 | 0.997 | 3.24 | 201 | 1.31 | 5.31 | 0.997 |
| 150 | 133 | 2.2 | 2.93 | 0.999 | 2.66 | 154 | 1.67 | 3.96 | 0.997 | |
| 125 | 113 | 1.7 | 1.92 | 0.999 | 1.67 | 136 | 1.36 | 2.50 | 0.992 | |
| 100 | 89 | 2.0 | 1.78 | 0.999 | 1.53 | 104 | 2.28 | 2.45 | 0.994 | |
| 75 | 67 | 2.5 | 1.68 | 1 | 1.36 | 76 | 3.97 | 2.32 | 0.990 | |
| 50 | 44 | 2 | 0.88 | 1 | 0.77 | 51 | 4.60 | 1.20 | 0.993 | |
| 60 | 200 | 170 | 3.4 | 5.79 | 1 | 4.7 | 190 | 2.33 | 8.44 | 0.993 |
| 150 | 128 | 3.4 | 4.35 | 0.999 | 3.61 | 146 | 2.85 | 6.10 | 0.996 | |
| 125 | 110 | 3.0 | 3.29 | 0.999 | 2.7 | 129 | 2.65 | 4.40 | 0.995 | |
| 100 | 88 | 3.3 | 2.91 | 0.999 | 2.23 | 99 | 4.32 | 4.22 | 0.991 | |
| 75 | 65 | 2.5 | 1.63 | 0.998 | 1.22 | 79 | 3.39 | 2.11 | 0.990 | |
| 50 | 43 | 3.4 | 1.46 | 1 | 1.2 | 49 | 8.38 | 2.05 | 0.995 | |
Была проведена также проверка выполнимости уравнения псевдовторого порядка:
где k2 – константа скорости псевдовторого порядка. Проверку проводили расчетным анализом нелинейной интегральной формы, полученной интегрированием уравнения (3):Выражение (4) для удобства использования в программе Mathcad было преобразовано в следующее:
используемое в подпрограмме minerr в виде где y = qt, a = qe, b = 1/k2qe, x = t.Несмотря на одинаково высокие значения коэффициентов корреляции, найденных для кинетических кривых, рассчитанных по обоим порядкам адсорбции, эти кривые не в одинаковой степени точно соответствуют экспериментальным данным. Это следует прежде всего из того, что значения qe, вычисленные по уравнению псевдовторого порядка, значительно (на 7–22 мг/г) превышают экспериментальные значения максимально достижимой адсорбции (в течение 10–25 ч). В то же время величины qe, рассчитанные по уравнению псевдопервого порядка, отличаются от этих экспериментальных значений не более чем на 4 мг/г. Для сравнения результатов расчетов кинетических параметров адсорбции СК на ГАУ по различным порядкам были определены начальные скорости адсорбции СК V0. Для уравнения псевдопервого порядка величину $V_{0}^{1}$ рассчитывали по формуле
для уравнения псевдовторого порядка аналогичный показатель $V_{0}^{2}$ вычисляли по формулеЭти величины сравнивали с начальной скоростью адсорбции СК, рассчитанной непосредственно из экспериментальных данных по формуле
где $q_{t}^{{15}}$ – адсорбция СК, измеренная после адсорбции в течение 15 мин. Сравнение величин $V_{0}^{1}$, $V_{0}^{2}$ и $V_{0}^{{{\text{эксп}}}}$, приведенных в табл. 1, показывает, что начальные скорости адсорбции, вычисленные по уравнению первого порядка, оказываются наиболее близкими к таковой, вычисленной непосредственно по начальному участку кинетический кривой адсорбции. Из этого можно сделать вывод, что только уравнение псевдопервого порядка адекватно описывает кинетику адсорбции СК на ГАУ.Сравнение кинетических кривых адсорбции СК, измеренных при равных начальных концентрациях СК при 25, 40 и 60°C, показывает, что, хотя максимальная адсорбция СК практически не зависит от температуры опыта, тем не менее для каждого данного момента времени адсорбция оказывается большей для более высокой температуры. Таким образом, скорость адсорбции растет с ростом температуры. Из температурной зависимости константы скорости адсорбции СК k1 от температуры для с0 = 200 мг/л (рис. 4) было найдено, что энергия активации адсорбции Еакт = = 26 кДж/моль, что указывает на то, что лимитирующая стадия адсорбции имеет диффузионную природу.
Из значений qe (табл. 1) по уравнению Ленгмюра
где qe – адсорбция СК, мг/г, отвечающая равновесной концентрации СК в растворе се, мг/л; qmax – емкость монослоя адсорбированной СК, мг/г; bL – коэффициент адсорбции, были построены изотермы адсорбции СК при различных температурах (рис. 5). Значения параметров уравнения Ленгмюра приведены в табл. 2.ЗАКЛЮЧЕНИЕ
Проведенные исследования показали, что ГАУ обладает высокой адсорбционной емкостью по отношению к СК. Максимальная адсорбционная емкость его по СК в несколько раз превышает указанную в литературе для других углеродных материалов [12–14]. В данной работе определено, что повышение температуры раствора от 25 до 60°C может увеличить скорость его извлечения более чем в 2 раза. ГАУ имеет более чем в 4 раза большую удельную поверхность по БЭТ, более чем в 3 раза начальную скорость адсорбции и более чем в 2 раза большую адсорбционную емкость (qe) по сравнению с образцом Сибунит [11].
Список литературы
Веденяпин А.А., Ракишев А.К., Веденяпина М.Д. Скундин А.М. // Изв. Академии промышленной экологии. 2007. № 1. С. 61.
Huppert N. Elimination von Ibuprofen und NBBS in kommunalen Kläranlagen analysiert mittels Festphasenmikroextraktion. Diss., Kahrlsruhe. 1999. P. 148.
Веденяпин А.А., Веденяпина М.Д., Ракишев А.К., Скундин А.М., Кулова Т.Л., Стрельцова Е.Д. // Конденсированные среды и межфазные границы. 2007. Т. 9. № 1. С. 26.
Веденяпина М.Д., Борисова Д.А., Ракишев А.К., Веденяпин А.А. // ХТТ. 2014. № 5. С. 51. [Solid Fuel Chemistry, 2014. V. 48. № 5. P. 323. https://doi.org/10.3103/S0361521914050139].https://doi.org/10.7868/S0023117714050132
Веденяпина М.Д., Стрельцова Е.Д., Виль В.А., Терентьев А.О., Веденяпин А.А. // ХТТ. 2016. № 5. С. 34. [Solid Fuel Chemistry, 2016. V. 50. P. 306. https://doi.org/10.3103/S0361521916050086].https://doi.org/10.7868/S002311771605008X
Веденяпина М.Д., Стопп П., Вайхгребе Д., Веденяпин А.А. // ХТТ. 2016. № 4. С. 61. [Solid Fuel Chemistry, 2016. V. 50. № 4. P. 265. https://doi.org/10.3103/S036152191604011X].https://doi.org/10.7868/S0023117716040113
Веденяпина М.Д., Стоп П., Вайхгребе Д., Веденяпин А.А. // ХТТ. 2016. № 1. С. 48. [Solid Fuel Chemistry, 2016. V. 50. № 1. P. 46. https://doi.org/10.3103/S0361521916010109].https://doi.org/10.7868/S0023117716010102
Веденяпина М.Д., Веденяпин А.А. // ХТТ. 2015. № 1. С. 44. [Solid Fuel Chemistry, 2015. V. 49. № 1. P. 41. https://doi.org/10.3103/S0361521915010127].https://doi.org/10.7868/S0023117715010132
Борисова Д.А., Веденяпина М.Д., Стрельцова Е.Д., Маслов В.Л., Розенвинкель К.-Х., Вайхгребе Д., Стопп П., Веденяпин А.А. // ХТТ. 2013. № 5. С. 46. [Solid Fuel Chemistry, 2013. V. 47. № 5. P. 298. https://doi.org/10.3103/S0361521913050030].https://doi.org/10.7868/S0023117713050034
Веденяпина М.Д., Борисова Д.А., Симакова А.П., Прошина Л.П., Веденяпин А.А. // ХТТ. 2013. № 1. С. 60. [Solid Fuel Chemistry, 2013. V. 47. № 1. P. 59. https://doi.org/10.3103/S0361521912060134].https://doi.org/10.7868/S002311771206014X
Веденяпина М.Д., Ракишев А.К., Цаплин Д.Е., Веденяпин А.А., Лапидус А.Л. // ХТТ. 2018. № 3. С. 41. [Solid Fuel Chemistry, 2018. V. 52. № 3. P. 179. https://doi.org/10.3103/S0361521918030126].https://doi.org/10.7868/S0023117718030064
Raoul T.T.D., Gabche A.S., Ndifor-Angwafor N.G., Mbadcam K.J. // International J. Current Engin. and Techn. 2015. V. 5. № 3. P. 1641.
Bernal V., Giraldo L., Moreno-Piraján J. C. // Environ. Sci. Pollut. R. 2020. V. 27. P. 36639.
Coimbra R.N., Calisto V., Ferreira C.I.A., Esteves V.I., Otero M. // Arab. J. Chem. 2019. V. 12. I. 8. P. 3611.
Vedenyapina M.D., Kurmysheva A.Yu., Rakishev A.K., Kryazhev Yu.G. // Solid Fuel Chem. 2019. V. 53. P. 382.
Mohammad-Pajooh E., Turcios A.E., Cuff G., Weichgrebe D., Rosenwinkel K.-H., Vedenyapina M.D., Sharifullina L.R. // J. Environ. Manage. 2018. V. 228. P. 189.
Xuejiao Liu, Yin Wang // Mater. Chem. Phys. 2019. V. 222. P. 369.
Кулайшин С.А., Веденяпина М.Д., Шарифуллина Л.Р., Лапидус А.Л. // ХТТ. 2020. № 1. С. 63. [Solid Fuel Chemistry, 2020. V. 54. № 1. P. 54. https://doi.org/10.3103/S0361521920010115].https://doi.org/10.31857/S0023117720010120
Веденяпина М.Д., Шарифуллина Л.Р., Кулайшин С.А., Веденяпин А.А., Лапидус А.Л. // Химия твердого топлива, 2017. № 2. С. 51. [Solid Fuel Chemistry, 2017. V. 51. № 2. P. 115. https://doi.org/10.3103/S0361521917020100].https://doi.org/10.7868/S0023117717020104
Качала В.В., Хемчян Л.Л., Кашин А.С., Орлов Н.В., Грачев А.А., Залесский С.С., Анаников В.П. // Успехи химии. 2013. Т. 82. С. 648.
Кашин А.С., Анаников В.П. // Изв. АН. Сер. хим. 2011. № 12. С. 2551.
Дополнительные материалы отсутствуют.
Инструменты
Химия твердого топлива





