Химия твердого топлива, 2021, № 1, стр. 3-10
КИНЕТИЧЕСКОЕ ИЗУЧЕНИЕ СТАДИЙНОСТИ ТЕРМИЧЕСКОГО РАЗЛОЖЕНИЯ РАЗЛИЧНЫХ УГЛЕЙ МОНГОЛИИ
О. Ю. Фетисова 1, *, П. Н. Кузнецов 1, **, Б. Пуревсурен 2, ***, Б. Авид 2, ****
1 Институт химии и химической технологии СО РАН, ФИЦ КНЦ СО РАН
660036 Красноярск, Россия
2 Институт химии и химической технологии Монгольской Академии наук
13330 Улан-Батор, Монголия
* E-mail: fetisova@icct.ru
** E-mail: kpn@akadem.ru
*** E-mail: bpurevsuren.icct@gmail.com
**** E-mail: avidmas@gmail.com
Поступила в редакцию 02.06.2020
После доработки 05.06.2020
Принята к публикации 07.10.2020
Аннотация
С помощью методов термического анализа (ТГ/ДТГ) исследован процесс термолиза углей Монголии различной степени метаморфизма. Установлена стадийность терморазложения в условиях программируемого нагрева до 1000°С в атмосфере аргона. На основе термогравиметрического анализа определены кинетические параметры пиролиза с помощью модельного (Коутса–Редферна) и безмодельного (Озавы–Флинна–Уолла) методов расчета. Установлено изменение энергии активации с увеличением степени разложения органической массы углей различной стадии метаморфизма. Выявлен кинетический компенсационный эффект, вероятно обусловленный многокомпонентным составом углей.
ВВЕДЕНИЕ
Монголия располагает значительными запасами углей разной стадии метаморфизма. Возможности их технологической переработки еще мало изучены. За последние годы все большее внимание уделяется проблеме создания способов технологической переработки с получением высококачественных и экологически безопасных энергоносителей и сырья для производства различных материалов.
Из угля можно получать широкий ассортимент продуктов, в том числе химические вещества, включая ароматические углеводороды, которые находят широкое применение при производстве углеродных, полимерных и пластиковых материалов и композитов. В настоящее время потребности этих отраслей в би- и полициклической ароматике обеспечиваются преимущественно компонентами коксохимической смолы – побочного продукта производства металлургического кокса для нужд черной металлургии.
В последние годы в большинстве стран наблюдается устойчивая тенденция уменьшения производства каменноугольной смолы из-за сокращения удельного расхода дорогостоящего металлургического кокса. Вместе с тем потребности в каменноугольной смоле как источнике ароматических углеводородов, требования к качеству непрерывно возрастают. Альтернативными процессами для их получения являются полукоксование углей и термическое растворение, которые позволяют получать широкий ассортимент углехимических продуктов как топливного, так и химического назначения.
Органическая масса углей содержит мономерные, олигомерные и мультимерные ароматические и гетероциклические молекулы, ассоциированные различными валентными сшивками и межмолекулярными взаимодействиями в полимероподобное твердое тело гетерогенного состава и нерегулярного пространственного строения. Вследствие сложного состава для создания эффективных и селективных процессов переработки важны детальные сведения о кинетике разложения их органической массы под действием температуры. При изучении кинетики пиролиза органических материалов широко используется термогравиметрический метод анализа (ТГА) как в изотермическом, так и в динамическом режимах [1–3]. Широкое распространение получил экспрессный метод динамической термогравиметрии. Предложенные способы определения кинетических параметров неизотермического пиролиза можно разделить на модельные (model-fitting) и безмодельные (model-free) или изоконверсионные. При применении модельного метода достаточно провести одно термоаналитическое измерение (метод Фримана–Кэррола [4], Коутса–Редферна [5]). В общем случае задача определения констант сводится к подбору и “подгонке” математической модели для скорости реакции под экспериментально полученную кинетическую кривую или ее отдельные участки. Безмодельные методы расчета кинетических параметров (метод Киссинджера [6], Киссинджера–Акахира–Суноз [7], Озавы–Флинн–Уолл [8, 9]) требуют построения кинетических кривых при разных скоростях нагрева. К несомненному их достоинству можно отнести возможность определения кинетических характеристик для каждого значения конверсии вещества, т.е. для разных этапов разложения.
Математические модели, используемые для определения кинетических характеристик деструкции полимеров, в приложении к пиролизу углей, вызывают определенные трудности из-за их сложного строения, многообразия типов химических связей и одновременно протекающих реакций [1–3,10], поэтому выработка рекомендаций для выбора и разработки адекватной кинетической модели пиролиза и формирование унифицированного банка данных кинетических характеристик являются важной исследовательской задачей.
Цель работы – исследование углей Монголии различной степени метаморфизма методами термического анализа и определение кинетических показателей термолиза с применением модельных (Коутса–Редферна) и безмодельных (Озавы–Флинн–Уолла) математических методов.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для исследования на угольных месторождениях Монголии (Багануур, Шиве-Овоо, Нарийнсухайт и Тавантолгой) были отобраны два образца бурых углей и два образца каменных углей. В опытах использовали измельченные (размер частиц <0.2 мм) и высушенные в вакуумном шкафу пробы. Влажность, зольность, содержание летучих веществ и показатель отражения витринита определяли по стандартным методикам. Элементный анализ осуществляли на анализаторе FlashEATM1112.
Термогравиметрическое исследование проводили с помощью прибора STA 449 F1 Jupiter (NETZSCH, Германия) в корундовых тиглях в интервале температур от 30 до 1000°С в потоке аргона (скорость потока защитного и продувочного газов 20 и 50 мл мин–1 соответственно). Обработка результатов измерений выполнена с помощью пакета программ “NETZSCH. ProteusThermalAnalysis.5.1.0”, поставляемого с прибором. Кинетические характеристики определяли на основе ТГ–данных при трех разных скоростях нагрева 5, 10 и 20 град мин–1.
Кинетическую обработку результатов ТГ/ДТГ анализа осуществляли с использованием двух методов расчета кинетических параметров: модельного (Коутса–Редферна, сокращенно КР) и безмодельного (Озавы–Флинн–Уолла, сокращенно ОФУ). Ранее указанные методы расчета кинетических параметров использовали при исследовании кинетики терморазложения лигнинов [11] и бурых углей [12].
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Характеристика углей. Показатели технического анализа и элементный состав использованных углей приведены в табл. 1.
Таблица 1.
Характеристики состава и свойств образцов углей
| Месторождение/ шифр образца угля | Аd,% | Vdaf,% | Элементный состав мас. % на daf | Показатель отражения витринита, Ro,% | ||||
|---|---|---|---|---|---|---|---|---|
| С | Н | N | S | О* | ||||
| Багануур/B | 5.1 | 44.7 | 70.9 | 5.2 | 1.0 | 0.5 | 22.4 | 0.41 |
| Шиве-Овоо/S | 18.7 | 44.8 | 73.1 | 4.3 | 1.0 | 0.9 | 20.7 | 0.46 |
| Нарийнсухайт/N | 6.8 | 35.7 | 82.1 | 4.7 | 13.2 | 0.74 | ||
| Тавантолгой/T | 8.2 | 27.7 | 87.8 | 5.2 | 1.2 | 0.4 | 5.4 | 1.12 |
Все угли характеризуются низким содержанием серы и азота. Содержание кислорода, в зависимости от типа угля, составляет от 22.4 до 5.4%, углерода от 70.9 до 87.8%, что указывает на разную степень их метаморфизма.
Все угли относятся к витринитовому типу с содержанием витринита более 80%. Коэффициенты отражения витринита составляют от 0.41 для угля B до 1.12% для угля Т, что отражает увеличение содержания полиароматических фрагментов в указанном ряду углей и степень их метаморфизма. Образцы углей В и S не спекаются, угли N и T обладают спекающими свойствами с толщиной пластического слоя 10 и 18 мм соответственно.
Данные ТГ/ДТГ. На рис. 1 приведены кривые термогравиметрического (ТГ) и дифференциально-термогравиметрического (ДТГ) анализа, показывающие зависимость убыли массы и скорости убыли массы от температуры. Из анализа кривых можно выделить три основных температурных этапа разложения углей, приведенных в табл. 2.
Таблица 2.
Данные термогравиметрического анализа образцов углей
| Образец | Температурный интервал, °С | Тmax, °С | Vmax, %/мин | Убыль массы, % | Убыль массы, мас. % на daf | Коксовый остаток при 1000°С, мас. % на daf |
|---|---|---|---|---|---|---|
| B | 30–239 | 110 | –0.65 | 6.90 | 7.3 | 55.0 |
| 239–655 | 440 | –1.61 | 31.37 | 33.2 | ||
| 655–1000 | – | – | 6.67 | 7.1 | ||
| S | 30–254 | 110 | –0.66 | 6.86 | 8.4 | 59.9 |
| 254–653 | 440 | –1.29 | 27.23 | 33.5 | ||
| 654–1000 | – | – | 6.13 | |||
| N | 30–335 | – | 2.6 | 2.8 | 67.1 | |
| 335–738 | 510 | –3.00 | 27.37 | 29.4 | ||
| 738–1000 | – | – | 2.91 | 3.1 | ||
| Т | 30–385 | – | – | 3.20 | 3.5 | 74.7 |
| 385–700 | 527 | –2.80 | 18.42 | 20.2 | ||
| 700–1000 | – | – | 3.72 | 4.1 |
1) Первый этап термолиза углей B и S характеризуется удалением влаги и окклюдированных газов в диапазоне температур: 30–239°С и 30–254°С, соответственно, с потерей массы 6.9%. Каменные угли N и T в указанном температурном интервале сравнительно устойчивы.
2) Второй этап соответствует процессу активного разложения органической массы углей с высокой скоростью выделения летучих веществ. На данном этапе происходит основная потеря массы: от 18.4 (для угля Т) до 31.4% (для угля B). С ростом углефикации температуры максимума основного разложения смещаются от 440°С для бурых углей до 527°С для угля Т (т.е. на 87°С) (табл. 2), что указывает на значительное уменьшение реакционной способности углей в процессе термодеструкции в указанном ряду.
3) Третий этап термолиза характеризуется медленными процессами дальнейшего разложения органических веществ. Низкометаморфизованные некоксующиеся угли В и S претерпевают более глубокую деструкцию, чем каменные N и T, величина коксового остатка для угля B уменьшается до 55.0%, против 74.7% для угля T.
Кинетическое исследование. Данные термогравиметрического анализа были использованы для расчета кинетических параметров термического разложения. Расчет основных кинетических параметров процесса выделения летучих веществ проведен с использованием двух методов: модельного (model-fitting) – Коутса–Редферна (КР) и безмодельного (model-free) – Озавы–Флинн–Уолла (ОФУ). Реакционная способность вещества может быть охарактеризована величиной энергии активации. Использование разных кинетических подходов предполагает получение более обоснованных величин энергий активации и других кинетических показателей.
Определение величины энергии активации основывалось на обобщенном выражении (1) скорости твердофазной реакции при неизотермических условиях:
(1)
$\frac{{d\alpha }}{{dT}} = \frac{A}{\beta }{{e}^{{\frac{{ - {{E}_{{\text{a}}}}}}{{RT}}}}}f(\alpha ),~~~$Метод Коутса–Редферна. Основное уравнение:
(2)
$\ln \left[ {\frac{{g(\alpha )}}{{{{T}^{2}}}}} \right] = \ln \left( {\frac{{AR}}{{\beta {{E}_{a}}}}} \right) - \frac{{{{E}_{a}}}}{{RT}}$,Графическое представление уравнения (2) для определения кинетических параметров термогравиметрических кривых реакции первого порядка использует следующеe уравнение:
(3)
$\ln \left[ { - \frac{{\ln (1 - \alpha )}}{{{{T}^{2}}}}} \right] = \ln \left( {\frac{{AR}}{{\beta E}}} \right) - \frac{E}{{RT}}$,Из приведенных в табл. 3 результатов расчетов видно, что для углей B и S значения энергии активации непрерывно растут с увеличением степени конверсии, соответственно, от 50 до 203 и от 75 до 210 кДж ⋅ моль–1.
Таблица 3.
Результаты кинетического анализа пиролиза углей методом Коутса–Редферна (R2 ≥ 0.889)
| Образец | Стадия | Температурный интервал, °С | Энергия активации, кДж/моль | Степень конверсии |
|---|---|---|---|---|
| B | I | 157–287 | 50 | 0.099–0.188 |
| II | 297–487 | 161 | 0.197–0.620 | |
| III | 497–707 | 203 | 0.642–0.896 | |
| S | I | 142–302 | 75 | 0.097–0.206 |
| II | 312–490 | 146 | 0.216–0.627 | |
| III | 502–722 | 210 | 0.651–0.904 | |
| N | I | 372–412 | 76 | 0.097–0.136 |
| II | 421–462 | 252 | 0.155–0.353 | |
| III | 473–533 | 100 | 0.391–0.573 | |
| IV | 540–733 | 154 | 0.586–0.904 | |
| Т | I | 348–407 | 75 | 0.100–0.152 |
| II | 417–479 | 264 | 0.166–0.378 | |
| III | 490–628 | 156 | 0.388–0.765 | |
| IV | 638–758 | 164 | 0.780–0.906 |
Для каменных углей N и T, после достижения α = 0.353 (462°С) и 0.378 (479°С), соответственно, наблюдается уменьшение энергии активации. Температурный интервал, характеризующийся пониженной энергией активации, для угля N примерно в 2 раза меньше, чем для угля T.
Метод Озавы–Флинн–Уолла. В основе метода ОФУ лежит предположение о том, что скорость реакции при постоянном значении α зависит только от температуры. При анализе неизотермической кинетики используют следующее уравнение:
(4)
$\ln {{\beta }_{i}} = \ln \left[ {\frac{{{{A}_{\alpha }}{{E}_{{\text{а}}}}}}{{Rg(\alpha )}}} \right] - 5.331 - 1.052\frac{{{{E}_{{\text{а}}}}}}{{R{{T}_{{\alpha ,{\text{i}}}}}}}$ .Отношение логарифма скорости нагрева (lnβ) к обратной температуре (1/Т) представляет прямую линию с наклоном, равным –1.052Ea/R.
Данные табл. 4 демонстрируют изменение Еа в диапазоне от 33 до 350 (для угля B), 30–386 (для S), 119–398 (для N), 126–475 (для T) кДж ⋅ моль–1, а частотный фактор (lnA) – в диапазоне от 0.8 до 37.8; 5.7 – 41.5; 17.7 – 48.1; 20.4 – 52.7 с–1 соответственно.
Таблица 4.
Энергии активации пиролиза углей (R2 ≥ 0.997)
| Относитель-ная степень конверсии, α | Багануур | Шиве-Овоо | Нарийнсухайт | Tавантолгой | ||||
|---|---|---|---|---|---|---|---|---|
| Еа, кДж/моль | lnA, c–1 | Еа, кДж/моль | lnA, c–1 | Еа, кДж/моль | lnA, c–1 | Еа, кДж/моль | lnA, c–1 | |
| 0.1 | 33 | 0.8 | 30 | 5.7 | 119 | 17.7 | 126 | 20.4 |
| 0.2 | 60 | 7.2 | 64 | 9.3 | 268 | 41.1 | 329 | 52.0 |
| 0.3 | 140 | 20.4 | 144 | 22.0 | 255 | 37.3 | 329 | 49.3 |
| 0.4 | 190 | 28.4 | 197 | 29.5 | 202 | 26.6 | 324 | 46.7 |
| 0.5 | 200 | 28.2 | 235 | 34.0 | 171 | 20.3 | 156 | 17.2 |
| 0.6 | 210 | 28.3 | 271 | 37.6 | 246 | 30.1 | 157 | 16.5 |
| 0.7 | 208 | 25.8 | 294 | 38.2 | 300 | 36.7 | 218 | 24.2 |
| 0.8 | 232 | 26.7 | 298 | 35.0 | 357 | 43.5 | 379 | 42.1 |
| 0.9 | 350 | 37.8 | 386 | 41.5 | 398 | 48.1 | 475 | 52.7 |
Рассчитанные значения показывают высокий коэффициент корреляции (R2 ≥ 0.997) и обеспечивают хорошую сходимость с экспериментальными данными. Значительные изменения энергии активации в ходе пиролиза свидетельствуют о смене лимитирующих стадий протекающих реакций, что обусловлено многокомпонентным и полифункциональным составом углей. Полученные величины попадают в интервал значений, приведенных в обзорной работе [13].
На рис. 2 рассчитанные величины Еа представлены в зависимости от степени термического разложения углей α. Видно, что в случае бурых углей B и S начальные стадии терморазложения протекают с низкой энергией активации, что может быть обусловлено расщеплением в первую очередь наиболее слабых кислородсодержащих связей в углях. Дальнейшее разложение органической массы с выделением летучих веществ при повышении температуры протекает со все более высокой энергией активации, т.е. в процесс деструкции вовлекаются термически все более устойчивые молекулярные фрагменты.
Терморазложение каменных углей (N и T) описывается более сложными кинетическими кривыми. Начальные стадии деструкции протекают с более высокой энергией активации, чем в случае бурых углей. Это может быть связано с тем, что каменные угли содержат значительно меньше кислорода, уже на начальном этапе происходит деструкция более прочных С–С алифатических связей. При повышении температуры деструкции подвергаются все более прочные связи, включая мостиковые сшивки между ароматическими фрагментами. Последующий этап разложения протекает с пониженной энергией активации. При разложении угля T этот этап начинается после достижения α = 0.4, в случае угля N он наступает уже после α = 0.2.
Одно из объяснений кинетических особенностей термолиза каменных углей в сравнении с бурыми может быть связано с тем, что разложение органической массы каменных углей приводит к образованию значительного количества поликонденсированных ароматических молекул и олигомеров. Последние, в силу низкой летучести, вместе с расплавленными битумами, содержащимися в исходных каменных углях, образуют жидкоподвижную пластичную массу, в которой диспергируются твердые разлагающиеся угольные частицы. С переходом термолиза в жидкую фазу значительно интенсифицируются конкурирующие процессы поликонденсации с зарождением и развитием нового твердого продукта – полукокса. В каждый момент реакции в пластической массе угля сосуществуют разлагающийся уголь, претерпевающая изменения жидкая фаза и образующаяся новая твердая фаза. Если на начальном этапе терморазложения ОМУ преобладал процесс деструкции, протекающий с повышенной энергией активации, то по мере накопления пластической массы и перехода реакции в жидкую фазу значительно интенсифицировались конкурирующие процессы поликонденсации, которые обычно экзотермичны [13] и протекают с невысокими энергиями активации.
Температурный диапазон существования пластического состояния различен для углей разной стадии метаморфизма. Уголь Тавантолгой, по данным Федоровой и Исмагилова [14], начинает размягчаться при температуре 429°С, затвердевание пластической массы происходит при 499°С, что практически соответствует температурному интервалу стадии термолиза с пониженной энергией активации. Для менее метаморфизованного угля N, судя по динамике энергии активации, он почти в два раза меньше. После отверждения пластической массы угольные частицы оказываются спекшимися в образовавшейся полукоксовой структуре. Дальнейшие реакции термолиза при повышении температуры происходят в твердой фазе с возрастающими значениями энергии активации, как и в случае твердофазного разложения бурых углей.
Возможно также, что стадия терморазложения каменных углей в температурном интервале пластического состояния и зарождения новой твердой фазы с пониженной величиной энергии активации может быть обусловлена влиянием диффузии жидких поликонденсированных ароматических молекул из объема спекшихся угольных частиц на их выход в газовую фазу.
Следует отметить, что каждый из используемых методов определения энергии активации в отдельности не всегда дает полностью удовлетворительные результаты. Основная причина тому – применение различных приближений и допущений в стремлении упростить модель расчета основных кинетических параметров. В связи с этим использование нескольких подходов для определения энергии активации термолиза углей способствует получению более надежных количественных результатов. Сравнение результатов расчета значений энергии активации пиролиза углей, методами КР и ОФУ (табл. 3 и 4 соответственно) показывает, что при приблизительно одинаковых конверсиях величины энергии активации по КР оказались меньше величин, полученных методом ОФУ, на 20–30%, при этом меньше и квадрат коэффициента корреляции. Кроме того, в литературе имеется ряд работ, в которых отмечены неудовлетворительные кинетические решения при применении model-fitting приемов [15, 16]. Вместе с тем для спекающихся углей оба метода выявляют уменьшение наблюдаемых энергий активации в области средних температур. Высокая корреляция экспериментальных данных (R2 ≥ 0.997), полученных методом ОФУ, позволяет говорить о применимости предложенных безмодельных методов оценки кинетики пиролиза углей в выбранных условиях.
Выявлена корреляционная связь между величиной энергии активации и предэкспоненциальным множителем, рассчитанными методом ОФУ. Из рис. 3 видно, что для всех углей эта зависимость описывается уравнением линейной регрессии вида: lnA = a + bE, где а и b – экспериментальные константы. Численные значения констант a и b, полученные обработкой данных методом наименьших квадратов, и соответствующие коэффициенты корреляции приведены в табл. 5.
Рис. 3.
Багануур (a), Шиве–Овоо (b), Нарийнсухайт (c), Тавантолгой (d). Зависимость величины предэкспоненциального множителя от энергии активации термолиза углей.
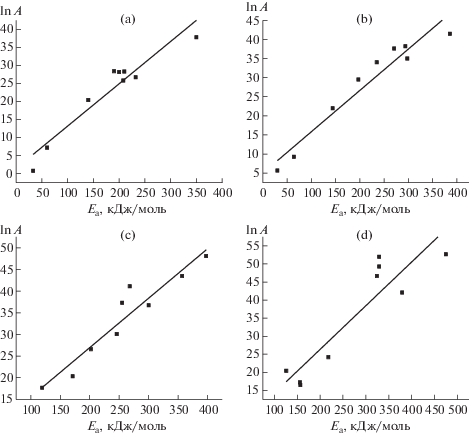
Таблица 5.
Экспериментальные константы в уравнении компенсационного эффекта в процессе термолиза углей
| Образец угля | Константа компенсационного эффекта | Коэффициент корреляции, R2 | |
|---|---|---|---|
| a | b | ||
| B | 0.1172 | 1.4853 | 0.902 |
| S | 0.1081 | 5.0424 | 0.929 |
| N | 0.1140 | 4.1505 | 0.896 |
| T | 0.1210 | 2.1519 | 0.809 |
Выведенные соотношения с высокими коэффициентами корреляции отражают проявление кинетического компенсационного эффекта, который может быть связан с различным содержанием определенных молекулярных групп в углях и с разной энергией активации их терморазложения.
ВЫВОДЫ
Получены данные о составе и термических свойствах образцов углей монгольских месторождений различной степени углефикации. Методом термического анализа в динамическом режиме при различных скоростях нагрева изучена динамика разложения органической массы.
По данным ТГ/ДТГ-анализа проведена оценка основного кинетического параметра реакции пиролиза – наблюдаемой энергии активации с использованием методов безмодельной (Озавы–Флинн–Уолла) и модельной (Коутса–Редферна) кинетики. Высокая корреляция экспериментальных данных (R2 ≥ 0.997), полученных методом Озавы–Флинна–Уолла, позволяет говорить о применимости предложенного безмодельного метода оценки кинетики пиролиза углей в выбранных условиях.
Для углей разной степени метаморфизма с помощью безмодельного метода Озавы–Флинн–Уолла определены особенности изменения энергии активации реакций терморазложения углей, протекающих на разных этапах разложения органической массы.
С помощью данных методов определены значения энергии активации пиролиза углей при различных степенях конверсии, что позволяет подробно интерпретировать данные термического анализа, выделяя стадии пиролиза.
Установлено наличие кинетического компенсационного эффекта, выведены уравнения линейной регрессии энергии активации и предэкспоненциального множителя.
Список литературы
Sangcheol Shin, Soo IkIm, Nam Sun Nho, Ki Bong Lee // J. Therm. Anal. Calorim. 2016. V. 126. P. 933.
Xu Y., Zhang Y., Wang Y., Zhang G., Chen L. // React. Kinet. Mech. Cat. 2013. V. 110. P. 225.
Марьяндышев П.А., Чернов А.А., Попова Е.И., Любов В.К. // ХTТ. 2016. № 3. С. 30. [Solid Fuel Chemistry, 2016, vol. 50, no. 3, p. 167–176. https://doi.org/10.3103/S0361521916030095].https://doi.org/10.7868/S0023117716030099
Freeman E.S., Carrol B. // J. Phys. Chem. 1958. V. 62. P. 394.
Coats A.W., Redfern J.P. // Nature. 1964. V. 201. P. 68.
Kissinger H.E. // Analyt. Chem. 1957. V. 29. I. 11. P. 1703.
Kissinger H.E. // J. Res. Nat. Bur. Stand. 1956. V. 57. P. 217.
Flynn J., Wall L. // J. Polym. Sci. Part B: Polym. Phys. 1966. V. 4. P. 323.
Ozawa T. // Bull. Chem. Soc. Jpn. 1965. V. 38. P. 1881.
Du Z., Sarofim A.F., Longwell J.P. // Energy and Fuels. 1990. V. 4. P. 296.
Фетисова О.Ю., Микова Н.М., Чесноков Н.В. // Кинетика и катализ. 2019. Т. 60. № 3. С. 289. [Kinetics and Catalysis, 2019, vol. 60, no. 3, p. 273–280. https://doi.org/10.1134/S0023158419030054].https://doi.org/10.1134/S0453881119030055
Фетисова О.Ю., Кузнецов П.Н., Чесноков Н.В. // Химия в инт. уст. развития. 2019. Т. 27. № 6. С. 677. https://doi.org/10.15372/KhUR2019190
Solomon P.R., Serio M.A. and Suuberg E.M. // Coal pyrolysis: Experiments, Kinetic rates and Mechanisms. Progress in Energy and Combustion Science. 1992. V. 18. P. 133.
Фёдорова Н.И., Манина Т.С., Исмагилов З.Р., Авид Б. // ХТТ. 2015. № 3. С. 3. [Solid Fuel Chemistry, 2015, vol. 49, no. 3, p. 129–134. https://doi.org/10.3103/S0361521915030064].
Ashraf A., Sattar H., Munir S. // Fuel. 2019. V. 240. P. 326.
Masnadi M.S., Habibi R., Kopyscinski J., Hill J.M., Bi X., Lim C.J., Ellis N., Grace J.R. // Fuel. 2014. V. 117. P. 1204.
Дополнительные материалы отсутствуют.
Инструменты
Химия твердого топлива




